MD5源码分析及流程

MD5算法实现：

输入：不定长度信息（要加密的信息）

输出：固定长度128-bits。由四个32位分组组成，将这四个32位分组级联后将生成一个128位散列值。

基本方式为：求余、取余、调整长度、与链接变量进行循环运算。得出结果。

填充

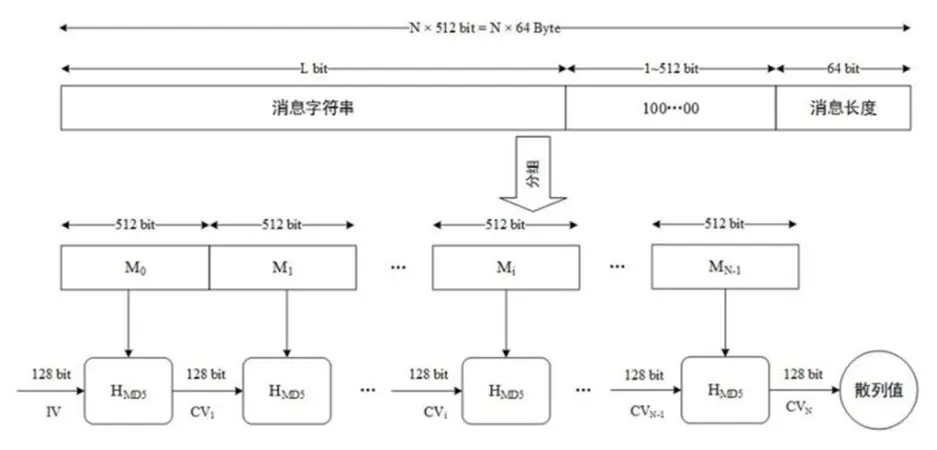
在MD5算法中，首先需要对输入信息进行填充，使其位长对512求余的结果等于448，并且填充必须进行，即使其位长对512求余的结果等于448。因此，信息的位长（Bits Length）将被扩展至N*512+448，N为一个非负整数，N可以是零。

填充的方法如下：

1. 在信息的后面填充一个1和无数个0，直到满足上面的条件时才停止用0对信息的填充。
2. 在这个结果后面附加一个以64位二进制表示的填充前信息长度（明文的长度，单位为Bit），如果二进制表示的填充前信息长度超过64位，则取低64位

经过这两步的处理，信息的位长=N512+448+64=(N+1）512，即长度恰好是512的整数倍。这样做的原因是为满足后面处理中对信息长度的要求。

初始化变量（变量值一般不变）

初始的128位值为初试链接变量，这些参数用于第一轮的运算，以大端字节序来表示，他们分别为：

A=0x01234567，

B=0x89ABCDEF，

C=0xFEDCBA98，

D=0x76543210。

（每一个变量给出的数值是高字节存于内存低地址，低字节存于内存高地址，即大端字节序。在程序中变量A、B、C、D的值分别为0x67452301，0xEFCDAB89，0x98BADCFE，0x10325476）

处理分组数据

消息分以512位为一分组进行处理，每一个分组进行上述4轮共64次计算后，将A，B，C，D分别加上计算得到的a，b，c，d。当做新的A，B，C，D，并将这4个变量赋值给a,b,c,d再进行下一分组的运算。由于填充后的消息长度为(N+1)*512，则共需计算N+1个分组。计算所有数据分组后，这4个变量为最后的结果，即MD5值。

每一分组的算法流程如下：

（1）第一分组需要将上面四个链接变量复制到另外四个变量中：A到a，B到b，C到c，D到d。

（2）从第二分组开始的变量为上一分组的运算结果，即A = a， B = b， C = c， D = d。

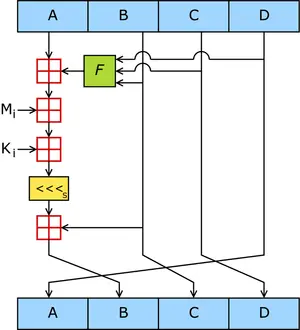
主循环有四轮（MD4只有三轮），每轮循环都很相似。第一轮进行16次操作。每次操作对a、b、c和d中的其中三个作一次非线性函数运算，然后将所得结果加上第四个变量，文本的一个子分组和一个常数。再将所得结果向左环移一个不定的数，并加上a、b、c或d中之一。最后用该结果取代a、b、c或d中之一。

一个MD5运算由类似的64次循环构成，分成4组16次。

F ：一个非线性函数，一个函数运算一次

Mi ：表示一个 32-bits 的输入数据

Ki：表示一个 32-bits 常数，用来完成每次不同的计算。

说明：

( (a + 线性函数(b,c,d) + Mj + Ki) << s) + a == B

以下是每次操作中用到的四个非线性函数（每轮一个）。

F( X ,Y ,Z ) = ( X & Y ) | ( (~X) & Z ) ==> If X then Y else Z

G( X ,Y ,Z ) = ( X & Z ) | ( Y & (~Z) ) ==> If Z then X else Y

H( X ,Y ,Z ) =X ^ Y ^ Z ==> If X=Y then Z else ~Z

I( X ,Y ,Z ) =Y ^ ( X | (~Z) )

（&是与（And），|是或（Or），~是非（Not），^是异或（Xor））

&	与	两个位都为1时，结果才为1
|	或	两个位都为0时，结果才为0
^	异或	两个位相同为0，相异为1
~	取反	0变1，1变0
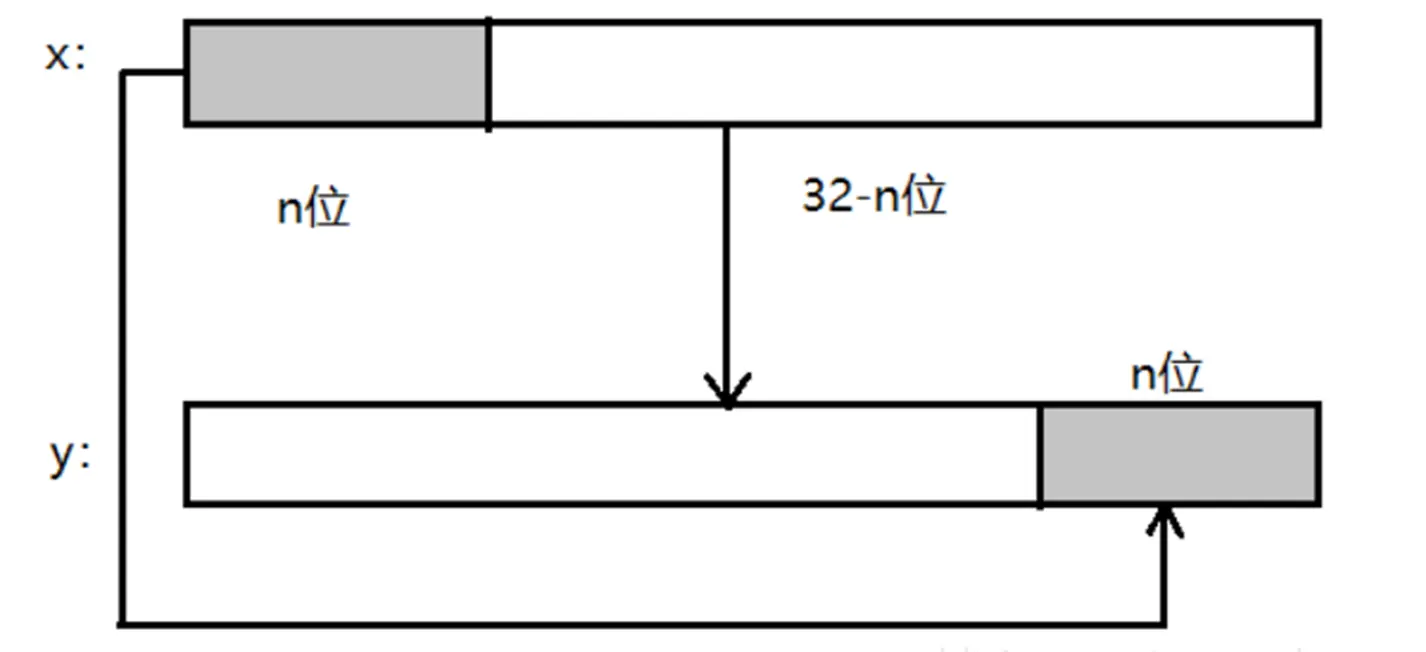
<<<	循环左移	将移出的低位放到该数的高位

循环左移:

这四个函数的说明：如果X、Y和Z的对应位是独立和均匀的，那么结果的每一位也应是独立和均匀的。

F是一个逐位运算的函数。即，如果X，那么Y，否则Z。函数H是逐位奇偶操作符。

假设Mj表示消息的第j个子分组（从0到15），常数ti是4294967296*abs( sin(i) ）的整数部分，i 取值从1到64，单位是弧度。（4294967296=2^(32)）

现定义：
FF(a ,b ,c ,d ,Mj ,s ,ti ) 操作为 a = b + ( (a + F(b,c,d) + Mj + ti) << s)
GG(a ,b ,c ,d ,Mj ,s ,ti ) 操作为 a = b + ( (a + G(b,c,d) + Mj + ti) << s)
HH(a ,b ,c ,d ,Mj ,s ,ti) 操作为 a = b + ( (a + H(b,c,d) + Mj + ti) << s)
II(a ,b ,c ,d ,Mj ,s ,ti) 操作为 a = b + ( (a + I(b,c,d) + Mj + ti) << s)

注意：“<<<”表示循环左移位，不是左移位

K表

[0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf,
 0x4787c62a, 0xa8304613, 0xfd469501, 0x698098d8, 0x8b44f7af,
 0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193, 0xa679438e,
 0x49b40821, 0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa,
 0xd62f105d, 0x2441453, 0xd8a1e681, 0xe7d3fbc8, 0x21e1cde6,
 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8,
 0x676f02d9, 0x8d2a4c8a, 0xfffa3942, 0x8771f681, 0x6d9d6122,
 0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70,
 0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x4881d05, 0xd9d4d039,
 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665, 0xf4292244, 0x432aff97,
 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92, 0xffeff47d,
 0x85845dd1, 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1,
 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391]

这四轮（共64步）是：
第一轮
FF(a ,b ,c ,d ,M0 ,7 ,0xd76aa478 )
FF(d ,a ,b ,c ,M1 ,12 ,0xe8c7b756 )
FF(c ,d ,a ,b ,M2 ,17 ,0x242070db )
FF(b ,c ,d ,a ,M3 ,22 ,0xc1bdceee )
FF(a ,b ,c ,d ,M4 ,7 ,0xf57c0faf )
FF(d ,a ,b ,c ,M5 ,12 ,0x4787c62a )
FF(c ,d ,a ,b ,M6 ,17 ,0xa8304613 )
FF(b ,c ,d ,a ,M7 ,22 ,0xfd469501)
FF(a ,b ,c ,d ,M8 ,7 ,0x698098d8 )
FF(d ,a ,b ,c ,M9 ,12 ,0x8b44f7af )
FF(c ,d ,a ,b ,M10 ,17 ,0xffff5bb1 )
FF(b ,c ,d ,a ,M11 ,22 ,0x895cd7be )
FF(a ,b ,c ,d ,M12 ,7 ,0x6b901122 )
FF(d ,a ,b ,c ,M13 ,12 ,0xfd987193 )
FF(c ,d ,a ,b ,M14 ,17 ,0xa679438e )
FF(b ,c ,d ,a ,M15 ,22 ,0x49b40821 )

第二轮
GG(a ,b ,c ,d ,M1 ,5 ,0xf61e2562 )
GG(d ,a ,b ,c ,M6 ,9 ,0xc040b340 )
GG(c ,d ,a ,b ,M11 ,14 ,0x265e5a51 )
GG(b ,c ,d ,a ,M0 ,20 ,0xe9b6c7aa )
GG(a ,b ,c ,d ,M5 ,5 ,0xd62f105d )
GG(d ,a ,b ,c ,M10 ,9 ,0x02441453 )
GG(c ,d ,a ,b ,M15 ,14 ,0xd8a1e681 )
GG(b ,c ,d ,a ,M4 ,20 ,0xe7d3fbc8 )
GG(a ,b ,c ,d ,M9 ,5 ,0x21e1cde6 )
GG(d ,a ,b ,c ,M14 ,9 ,0xc33707d6 )
GG(c ,d ,a ,b ,M3 ,14 ,0xf4d50d87 )
GG(b ,c ,d ,a ,M8 ,20 ,0x455a14ed )
GG(a ,b ,c ,d ,M13 ,5 ,0xa9e3e905 )
GG(d ,a ,b ,c ,M2 ,9 ,0xfcefa3f8 )
GG(c ,d ,a ,b ,M7 ,14 ,0x676f02d9 )
GG(b ,c ,d ,a ,M12 ,20 ,0x8d2a4c8a}

第三轮
HH(a ,b ,c ,d ,M5 ,4 ,0xfffa3942 )
HH(d ,a ,b ,c ,M8 ,11 ,0x8771f681 )
HH(c ,d ,a ,b ,M11 ,16 ,0x6d9d6122 )
HH(b ,c ,d ,a ,M14 ,23 ,0xfde5380c )
HH(a ,b ,c ,d ,M1 ,4 ,0xa4beea44 )
HH(d ,a ,b ,c ,M4 ,11 ,0x4bdecfa9 )
HH(c ,d ,a ,b ,M7 ,16 ,0xf6bb4b60 )
HH(b ,c ,d ,a ,M10 ,23 ,0xbebfbc70 }
HH(a ,b ,c ,d ,M13 ,4 ,0x289b7ec6 )
HH(d ,a ,b ,c ,M0 ,11 ,0xeaa127fa )
HH(c ,d ,a ,b ,M3 ,16 ,0xd4ef3085 )
HH(b ,c ,d ,a ,M6 ,23 ,0x04881d05 )
HH(a ,b ,c ,d ,M9 ,4 ,0xd9d4d039 )
HH(d ,a ,b ,c ,M12 ,11 ,0xe6db99e5 )
HH(c ,d ,a ,b ,M15 ,16 ,0x1fa27cf8 )
HH(b ,c ,d ,a ,M2 ,23 ,0xc4ac5665 )

第四轮
II(a ,b ,c ,d ,M0 ,6 ,0xf4292244 )
II(d ,a ,b ,c ,M7 ,10 ,0x432aff97 )
II(c ,d ,a ,b ,M14 ,15 ,0xab9423a7 )
II(b ,c ,d ,a ,M5 ,21 ,0xfc93a039 )
II(a ,b ,c ,d ,M12 ,6 ,0x655b59c3 )
II(d ,a ,b ,c ,M3 ,10 ,0x8f0ccc92 )
II(c ,d ,a ,b ,M10 ,15 ,0xffeff47d )
II(b ,c ,d ,a ,M1 ,21 ,0x85845dd1 )
II(a ,b ,c ,d ,M8 ,6 ,0x6fa87e4f )
II(d ,a ,b ,c ,M15 ,10 ,0xfe2ce6e0 )
II(c ,d ,a ,b ,M6 ,15 ,0xa3014314 )
II(b ,c ,d ,a ,M13 ,21 ,0x4e0811a1 )
II(a ,b ,c ,d ,M4 ,6 ,0xf7537e82 )
II(d ,a ,b ,c ,M11 ,10 ,0xbd3af235 )
II(c ,d ,a ,b ,M2 ,15 ,0x2ad7d2bb )
II(b ,c ,d ,a ,M9 ,21 ,0xeb86d391 )

所有这些完成之后，将a、b、c、d分别在原来基础上再加上A、B、C、D。

即a = a + A，b = b + B，c = c + C，d = d + D

然后用下一分组数据继续运行以上算法。

输出

最后的输出是a、b、c和d的大端法级联。

例子：123456 进行md5

123456==>ASCII 31 32 33 34 35 36

转为二进制就是 4*12 = 48bit

31 ==> 0011 0001

32 ==> 0011 0010

33 ==> 0011 0011

34 ==> 0011 0100

35 ==> 0011 0101

36 ==> 0011 0110


48bit填充1000….到448bit 填充1个1和399个0

0011 0001 0011 0010 0011 0011 0011 0100 0011 0101 0011 0110 1000000….

对应16进制

31 32 33 34 35 36 80 …..（98个0）

512bit - 448bit = 64bit

留的那64比特长度，用于填充长度信息，长度单位为比特

64bit附加长度信息 （就是明文对应16进制的长度）

00 …. 48（60个0）以小端法存放==》 48 00 … 00

明文48bit+填充（10…）400bit+长度信息（48 00..）64bit = 512bit

31 32 33 34 35 36 80 00 … 30 00 ..

512bit / 4 = 128位16进制

128分16组 = 8位 （每组8位）

M1 ==> 31 32 33 34

M2 ==> 35 36 80 00

M3 ==> 00 00 00 00

…


M15 ==> 30 00 00 00

M16 ==> 00 00 00 00


初始值变量

A=0x 01 23 45 67，

B=0x 89 AB CD EF，

C=0x FE DC BA 98，

D=0x 76 54 32 10。


以小端法存储

A ==> 0x 67 45 23 01

B ==> 0x EF CD AB 89

C ==> 0x 98 BA DC FE

D ==> 0x 10 32 54 76


二进制

A => 0110 0111 0100 0101 0011 0010 0000 0001

B => 1110 1111 1100 1101 1010 1011 1000 1001

C => 1001 1000 1011 1010 1101 1100 1111 1110

D => 0001 0000 0011 0010 0101 0100 0111 0110


第一轮第一步

FF(a ,b ,c ,d ,M0 ,7 ,0xd76aa478 )

b + ( (a + F(b,c,d) + Mj + Ki) << s)

F(b,c,d) == > ( X & Y ) | ( (~X) & Z ) ==> If X then Y else Z


F(b,c,d) ==> 1001 1000 1011 1010 1101 1100 1111 1110 ==> 98 BA DC FE

+a => 98 BA DC FE + 67 45 23 01 => FF FF FF FF

M1 = 31 32 33 34 小端法 => 34 33 32 31

+M1 => FF FF FF FF + 34 33 32 31 => 34 33 32 30 (只保留低8位)



+Ki==> 34 33 32 30 + D7 6A A4 78 => 0B 9D D6 A8 ==> 0000 1011 1001 1101 1101 0110 1010 1000



<<<s(7)

==> 0011 1011 1010 1101 0101 0000 0001 0111 ==> CE EB 54 05

+b

==> CE EB 54 05 + EF CD AB 89 ==> BE B8 FF 8E

第一轮后

a ==> 0x 10 32 54 76

b ==> 0x DE B8 FF 8E

c ==> 0x EF CD AB 89

d ==> 0x 98 BA DC FE

…


第64轮

a ==> 0x B7 E8 71 AF ==> 1011 0111 1110 1000 0111 0001 1010 1111

b ==> 0x BF 25 79 C0 ==> 1011 1111 0010 0101 0111 1001 1100 0000

c ==> 0x 2E 55 BB 7C ==> 0010 1110 0101 0101 1011 1011 0111 1100

d ==> 0x D2 96 E7 E0 ==> 1101 0010 1001 0110 1110 0111 1110 0000

b + ( (a + I(b,c,d) + Mj + ti) << s)

I(b,c,d) ==> I( b ,c ,d ) =c ^ ( b | (d) ) ==>

(d) ==> 0010 1101 0110 1001 0001 1000 0001 1111

b | (~d) ==> 1011 1111 0110 1101 0111 1001 1101 1111

c ^ ( b | (~d) ) ==> 1001 0001 0011 1000 1100 0010 1010 0011 ==> 91 38 C2 A3

+a ==> 0x 49 21 34 52

M64 = 0

+M64 ==> 0x 49 21 34 52

K64 = 0x EB 86 D3 91

+K64 ==> 0x 34 A8 07 E3 ==> 0011 0100 1010 1000 0000 0111 1110 0011

s64 = 21

<< s ==> 1111 1100 0110 0110 1001 0101 0000 0000 ==> 0x FC 66 95 00

+b ==> 0x BB 8C 0E C0

a == d ==0x D2 96 E7 E0

b ==0x BB 8C 0E C0

c == b ==0x BF 25 79 C0

d == c ==0x 2E 55 BB 7C

将a、b、c、d分别在原来基础上再加上A、B、C、D。

即a = a + A，b = b + B，c = c + C，d = d + D

a = a + A ==> 0x 39 DC 0A E1 ==> 0x E1 0A DC 39

b = b + B ==> 0x AB 59 BA 49 ==> 0x 49 BA 59 AB

c = c + C ==> 0x 57 E0 56 BE ==> 0x BE 56 E0 57

d = d + D ==>0x 3E 88 0F F2 ==> 0x F2 0F 88 3E

abcd == E1 0A DC 39 49 BA 59 AB BE 56 E0 57 F2 0F 88 3E => e10adc3949ba59abbe56e057f20f883e

MD5相对MD4所作的改进：

1.增加了第四轮.

2.每一步均有唯一的加法常数.

3.为减弱第二轮中函数G的对称性从(X&Y)|(X&Z)|(Y&Z)变为(X&Z)|(Y&(~Z))

4.第一步加上了上一步的结果,这将引起更快的雪崩效应.

5.改变了第二轮和第三轮中访问消息子分组的次序,使其更不相似.

6.近似优化了每一轮中的循环左移位移量以实现更快的雪崩效应.各轮的位移量互不相同.

对明文编码

为什么是这些非线性函数？

Ø这没什么最优解，你也可以使用别的非线性函数，或者自己实现时把顺序颠倒

Ø但这可能会造成算法安全性下降，而且是你无法把控的部分，因为这部分内容的专业性非常强，属于密码学的内容

为什么K表是这样，sin函数，或者说三角函数，在这儿扮演了怎样的角色？

k表的生成是： Ki = 2^32 x |sin i|

截取整数转16进制

例如：K1 = 2^32 x |sin 1| = 3614090360.2828…..

3614090360 ==> D76AA478

循环左移为什么是这样移？这个规定是为什么呢？(随机)

我们只知道，本质上，它是为了更好的扩散和混淆，让明文和密文之间没有明显的对应和关联，但为什么这样做，可能是安全性上的考量

比如胎死腹中的sha0和被广泛使用的sha1，竟然只通过循环左移1位就解决了安全性的问题

为什么是填充1个1和其余都是0，不是都是0

加入输入 1000

填充都是0后 1000 0000

不知道明文是哪个了

填充1后 1000 1000

就可以区分出来

大端、小端基础知识

https://zhuanlan.zhihu.com/p/316347205

python md5

import binascii
import sys
import os.path

SV = [0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf,
      0x4787c62a, 0xa8304613, 0xfd469501, 0x698098d8, 0x8b44f7af,
      0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193, 0xa679438e,
      0x49b40821, 0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa,
      0xd62f105d, 0x2441453, 0xd8a1e681, 0xe7d3fbc8, 0x21e1cde6,
      0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8,
      0x676f02d9, 0x8d2a4c8a, 0xfffa3942, 0x8771f681, 0x6d9d6122,
      0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70,
      0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x4881d05, 0xd9d4d039,
      0xe6db99e5, 0x1fa27cf8, 0xc4ac5665, 0xf4292244, 0x432aff97,
      0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92, 0xffeff47d,
      0x85845dd1, 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1,
      0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391]


# 根据ascil编码把字符转成对应的二进制
def binvalue(val, bitsize):
    binval = bin(val)[2:] if isinstance(val, int) else bin(ord(val))[2:]
    if len(binval) > bitsize:
        raise ("binary value larger than the expected size")
    while len(binval) < bitsize:
        binval = "0" + binval
    return binval


def string_to_bit_array(text):
    array = list()
    for char in text:
        binval = binvalue(char, 8)
        array.extend([int(x) for x in list(binval)])
    return array


# 循环左移
def leftCircularShift(k, bits):
    bits = bits % 32
    k = k % (2 ** 32)
    upper = (k << bits) % (2 ** 32)
    result = upper | (k >> (32 - (bits)))
    return (result)


# 分块
def blockDivide(block, chunks):
    result = []
    size = len(block) // chunks
    for i in range(0, chunks):
        result.append(int.from_bytes(block[i * size:(i + 1) * size], byteorder="little"))
    return result


# F函数作用于“比特位”上
# if x then y else z
def F(X, Y, Z):
    return ((X & Y) | ((~X) & Z))


# if z then x else y
def G(X, Y, Z):
    return ((X & Z) | (Y & (~Z)))


# if X = Y then Z else ~Z
def H(X, Y, Z):
    return (X ^ Y ^ Z)


def I(X, Y, Z):
    return (Y ^ (X | (~Z)))


# 四个F函数
def FF(a, b, c, d, M, s, t):
    result = b + leftCircularShift((a + F(b, c, d) + M + t), s)
    return (result)


def GG(a, b, c, d, M, s, t):
    result = b + leftCircularShift((a + G(b, c, d) + M + t), s)
    return (result)


def HH(a, b, c, d, M, s, t):
    result = b + leftCircularShift((a + H(b, c, d) + M + t), s)
    return (result)


def II(a, b, c, d, M, s, t):
    result = b + leftCircularShift((a + I(b, c, d) + M + t), s)
    return (result)


# 数据转换
def fmt8(num):
    bighex = "{0:08x}".format(num)
    binver = binascii.unhexlify(bighex)
    result = "{0:08x}".format(int.from_bytes(binver, byteorder='little'))
    return (result)


# 计算比特长度
def bitlen(bitstring):
    return len(bitstring) * 8


def md5sum(msg):
    # 计算比特长度，如果内容过长，64个比特放不下。就取低64bit。
    msgLen = bitlen(msg) % (2 ** 64)
    # 先填充一个0x80，其实是先填充一个1，后面跟对应个数的0，因为一个明文的编码至少需要8比特，所以直接填充 0b10000000即0x80
    msg = msg + b'\x80'  # 0x80 = 1000 0000
    # 似乎各种编码，即使是一个字母，都至少得1个字节，即8bit才能表示，所以不会出现原文55bit，pad1就满足的情况？可是不对呀，要是二进制文件呢？
    # 填充0到满足要求为止。
    zeroPad = (448 - (msgLen + 8) % 512) % 512
    zeroPad //= 8
    msg = msg + b'\x00' * zeroPad + msgLen.to_bytes(8, byteorder='little')
    # 计算循环轮数，512个为一轮
    msgLen = bitlen(msg)
    iterations = msgLen // 512
    # 初始化变量
    # 算法魔改的第一个点，也是最明显的点
    A = 0x67452301
    B = 0xefcdab89
    C = 0x98badcfe
    D = 0x10325476
    # MD5的主体就是对abcd进行n次的迭代，所以得有个初始值，可以随便选，也可以用默认的魔数，这个改起来毫无风险，所以大家爱魔改它，甚至改这个都不算魔改。
    # main loop
    for i in range(0, iterations):
        a = A
        b = B
        c = C
        d = D
        block = msg[i * 64:(i + 1) * 64]
        # 明文的处理，顺便调整了一下端序
        M = blockDivide(block, 16)
        # Rounds
        a = FF(a, b, c, d, M[0], 7, SV[0])
        d = FF(d, a, b, c, M[1], 12, SV[1])
        c = FF(c, d, a, b, M[2], 17, SV[2])
        b = FF(b, c, d, a, M[3], 22, SV[3])
        a = FF(a, b, c, d, M[4], 7, SV[4])
        d = FF(d, a, b, c, M[5], 12, SV[5])
        c = FF(c, d, a, b, M[6], 17, SV[6])
        b = FF(b, c, d, a, M[7], 22, SV[7])
        a = FF(a, b, c, d, M[8], 7, SV[8])
        d = FF(d, a, b, c, M[9], 12, SV[9])
        c = FF(c, d, a, b, M[10], 17, SV[10])
        b = FF(b, c, d, a, M[11], 22, SV[11])
        a = FF(a, b, c, d, M[12], 7, SV[12])
        d = FF(d, a, b, c, M[13], 12, SV[13])
        c = FF(c, d, a, b, M[14], 17, SV[14])
        b = FF(b, c, d, a, M[15], 22, SV[15])

        a = GG(a, b, c, d, M[1], 5, SV[16])
        d = GG(d, a, b, c, M[6], 9, SV[17])
        c = GG(c, d, a, b, M[11], 14, SV[18])
        b = GG(b, c, d, a, M[0], 20, SV[19])
        a = GG(a, b, c, d, M[5], 5, SV[20])
        d = GG(d, a, b, c, M[10], 9, SV[21])
        c = GG(c, d, a, b, M[15], 14, SV[22])
        b = GG(b, c, d, a, M[4], 20, SV[23])
        a = GG(a, b, c, d, M[9], 5, SV[24])
        d = GG(d, a, b, c, M[14], 9, SV[25])
        c = GG(c, d, a, b, M[3], 14, SV[26])
        b = GG(b, c, d, a, M[8], 20, SV[27])
        a = GG(a, b, c, d, M[13], 5, SV[28])
        d = GG(d, a, b, c, M[2], 9, SV[29])
        c = GG(c, d, a, b, M[7], 14, SV[30])
        b = GG(b, c, d, a, M[12], 20, SV[31])

        a = HH(a, b, c, d, M[5], 4, SV[32])
        d = HH(d, a, b, c, M[8], 11, SV[33])
        c = HH(c, d, a, b, M[11], 16, SV[34])
        b = HH(b, c, d, a, M[14], 23, SV[35])
        a = HH(a, b, c, d, M[1], 4, SV[36])
        d = HH(d, a, b, c, M[4], 11, SV[37])
        c = HH(c, d, a, b, M[7], 16, SV[38])
        b = HH(b, c, d, a, M[10], 23, SV[39])
        a = HH(a, b, c, d, M[13], 4, SV[40])
        d = HH(d, a, b, c, M[0], 11, SV[41])
        c = HH(c, d, a, b, M[3], 16, SV[42])
        b = HH(b, c, d, a, M[6], 23, SV[43])
        a = HH(a, b, c, d, M[9], 4, SV[44])
        d = HH(d, a, b, c, M[12], 11, SV[45])
        c = HH(c, d, a, b, M[15], 16, SV[46])
        b = HH(b, c, d, a, M[2], 23, SV[47])

        a = II(a, b, c, d, M[0], 6, SV[48])
        d = II(d, a, b, c, M[7], 10, SV[49])
        c = II(c, d, a, b, M[14], 15, SV[50])
        b = II(b, c, d, a, M[5], 21, SV[51])
        a = II(a, b, c, d, M[12], 6, SV[52])
        d = II(d, a, b, c, M[3], 10, SV[53])
        c = II(c, d, a, b, M[10], 15, SV[54])
        b = II(b, c, d, a, M[1], 21, SV[55])
        a = II(a, b, c, d, M[8], 6, SV[56])
        d = II(d, a, b, c, M[15], 10, SV[57])
        c = II(c, d, a, b, M[6], 15, SV[58])
        b = II(b, c, d, a, M[13], 21, SV[59])
        a = II(a, b, c, d, M[4], 6, SV[60])
        d = II(d, a, b, c, M[11], 10, SV[61])
        c = II(c, d, a, b, M[2], 15, SV[62])
        b = II(b, c, d, a, M[9], 21, SV[63])
        A = (A + a) % (2 ** 32)
        B = (B + b) % (2 ** 32)
        C = (C + c) % (2 ** 32)
        D = (D + d) % (2 ** 32)
    result = fmt8(A) + fmt8(B) + fmt8(C) + fmt8(D)
    return result


if __name__ == "__main__":
    data = str("123456").encode("UTF-8")
    print("plainText: ", data)
    print("result: ", md5sum(data))