AES知道某一轮次密钥反推主密钥

从轮密钥逆推主密钥

首先讨论AES-128
这里用上上篇对称加密算法AES原理及分析里面用到的密钥0123456789abcdef0123456789abcdef生成的10轮子密钥做分析

K00:0123456789abcdef0123456789abcdef
K01:629e9ac0eb35572fea16124863bddfa7
K02:1a00c63bf13591141b23835c789e5cfb
K03:154ac987e47f5893ff5cdbcf87c28734
K04:385dd190dc228903237e52cca4bcd5f8
K05:4d5e90d9917c19dab2024b1616be9eee
K06:c355b89e5229a144e02bea52f69574bc
K07:a9c7dddcfbee7c981bc596caed50e276
K08:7a5fe58981b199119a740fdb7724edad
K09:570a707cd6bbe96d4ccfe6b63beb0b1b
K10:8821df9e5e9a36f31255d04529bedb5e

假如获取到的是K0，那不用说。如果获取到的是K10呢？
8821df9e5e9a36f31255d04529bedb5e，首先我们会到W数组的视图，看W10密钥怎么编排出来的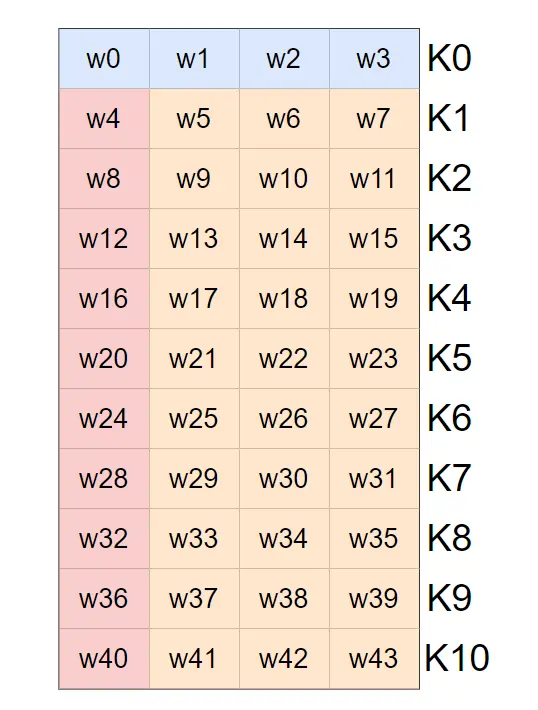

K10是W40,W41,W42,W43拼起来的，我们已知K10，即已知W40,W41,W42,W43有没有办法求K9？如果可以，那么同理可以逆推到K0，即求得了主密钥

我们不妨先复习一下异或的基本性质，异或作用与比特位上，对应的比特位相同则为0，相异则为1。

因为相同为0，相异为1，那么一个数和自身异或时，因为每个比特位都相同，所以结果为0。

而当某个数和0异或时，自身为0的比特0^0得0，自身为1的比特位1^0得1，这就导致结果和没异或前一样。

除此之外，异或并不看谁先谁后，A ^ B 与 B ^ A 显然无区别，即具有交换律。

看看异或的多角度理解：如何理解「异或」的含义。
下面做变换，左右W42异或

K10中涉及到的四个式子均可以做变化

K10 = 8821df9e5e9a36f31255d04529bedb5e，切成四块

W40 = 8821df9e W41 = 5e9a36f3 W42 = 1255d045 W43 = 29bedb5e

>>> hex(0x8821df9e^0x5e9a36f3)
'0xd6bbe96d'
>>> hex(0x5e9a36f3^0x1255d045)
'0x4ccfe6b6'
>>> hex(0x1255d045^0x29bedb5e)
'0x3beb0b1b'

所以
W37 = 0xd6bbe96d
W38 = 0x4ccfe6b6
W39 = 0x3beb0b1b
求出了W37,W38,W39，即K9的后大半部分，和真实情况比对后发现一致。
K09:570a707cd6bbe96d4ccfe6b63beb0b1b
那么W36呢？再复习一下g函数吧
首先循环左移一字节，3beb0b1b 变成 eb0b1b3b
然后逐字节S盒替换，得e92bafe2

>>> SBox = [
...     0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
...     0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
...     0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
...     0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
...     0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
...     0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
...     0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
...     0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
...     0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
...     0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
...     0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
...     0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
...     0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
...     0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
...     0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
...     0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16
... ]
>>> hex(SBox[0xeb])
'0xe9'
>>> hex(SBox[0x0b])
'0x2b'
>>> hex(SBox[0x1b])
'0xaf'
>>> hex(SBox[0x3b])
'0xe2'

最后是首字节和Rcon中的一个字节异或，这是最后一次变换，即用0x36

1	rcon = [0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36]

即

1 2	>>> hex(0xe9^0x36) '0xdf'

g函数的结果即是0xdf2bafe2
那上面W36=g(W39) xor W40 = 0xdf2bafe2 xor 0x8821df9e

1 2	>>> hex(0xdf2bafe2^0x8821df9e) '0x570a707c'

所以完整的K9：570a707cd6bbe96d4ccfe6b63beb0b1b，就被我们分析出来了，跟一开始的K表里的K9是一致的。可以继续往上推出K0，获得主密钥。即AES可以依靠轮密钥逆推出主密钥。严肃的说，AES-128可以通过一轮轮密钥逆推出主密钥，AES-192需要一轮半，AES-256需要两轮轮密钥。

接下来顺便下讨论DES的

DES密钥长八字节，在密钥编排时，会舍弃每个字节的最后1比特。因此实际参与密钥编排的是56比特，我们可以验证这一点。
假设密钥是

1	11 22 33 44 55 66 77 88 (hex)

二进制即
00010001 00100010 00110011 01000100 01010101 01100110 01110111 10001000
我们将末尾1比特翻转，即0变1，1变0。如果AES密钥中每个字节的最后一位被“丢弃”，那么翻转后也并不会对程序有任何影响，反之加密结果应该不同。
00010000 00100011 00110010 01000101 01010100 01100111 01110110 10001001
转成十六进制即

1	10 23 32 45 54 67 76 89 (hex)

在Cyberchef中，使用这两个密钥进行DES加密，结果完全一致。

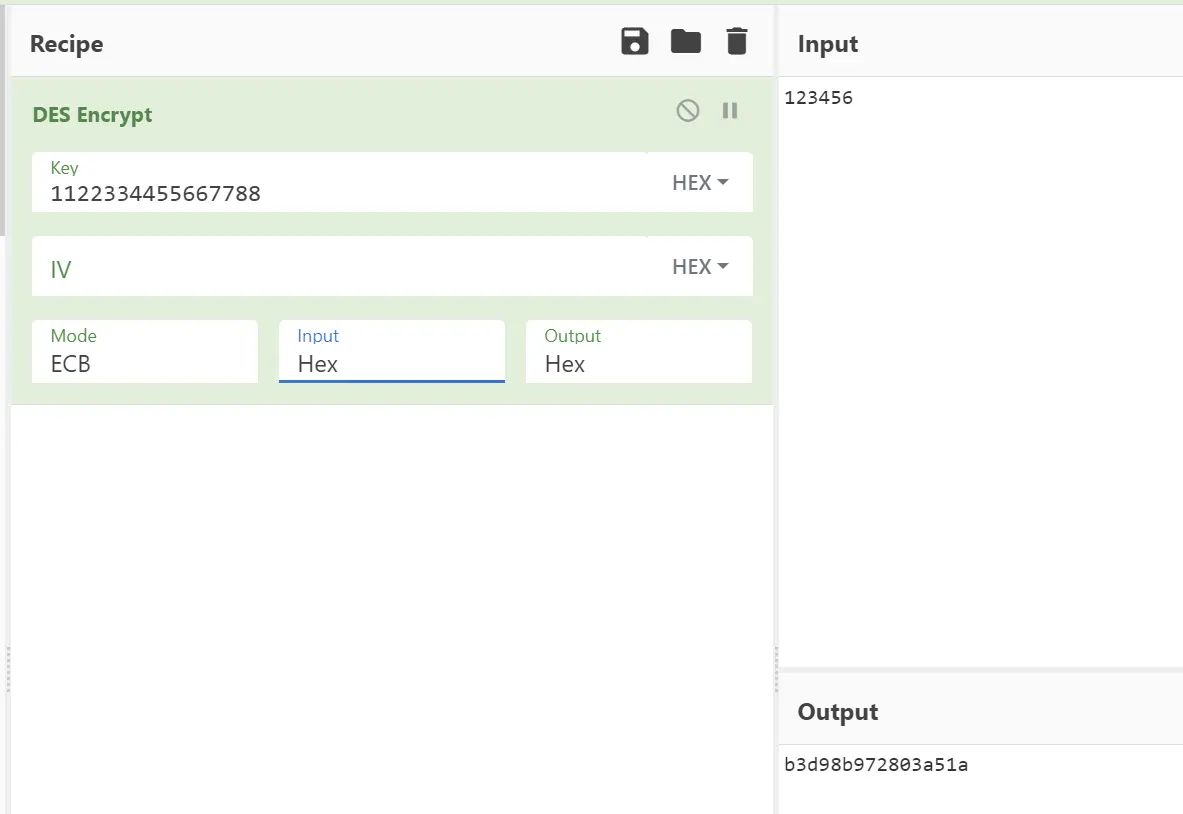
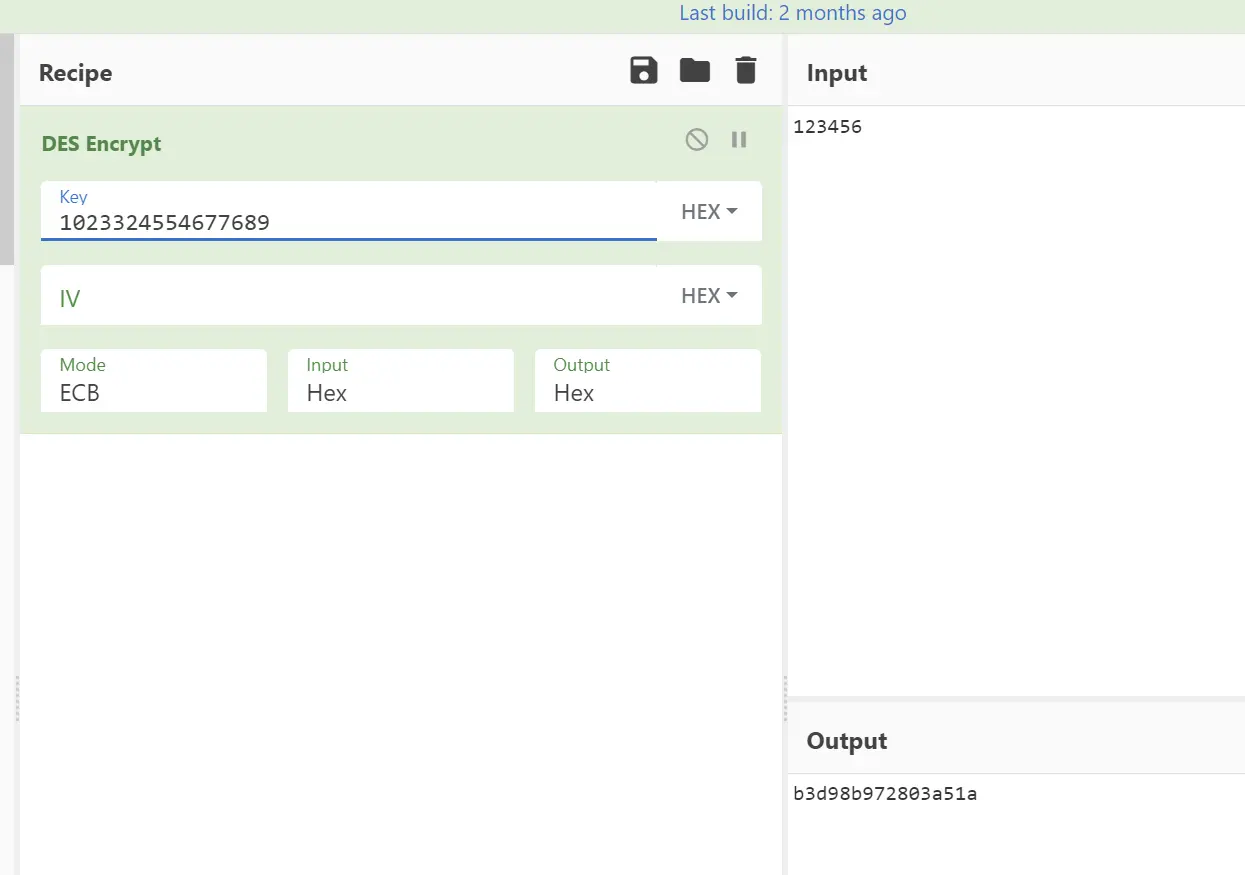
对于DES而言，已知两轮或两轮以上的子密钥，就可逆推出初始密钥，具体代码见 DES 子密钥逆推初始密钥一文。对于主密钥中无法复原的八比特，随便补什么都行，反正不影响结果。
在实际场景中，当我们需要基于AES/DES的轮密钥恢复主密钥时，我们用 SideChannelMarvels/Stark 这个开源项目，用户体验很好。
在另外一些情况中，目标加密算法可以基于某个轮密钥逆推出全体轮密钥，但没法恢复出主密钥，那怎么办呢——这不就是一开始说的吗

轮密钥所处的内存块可区分吗

首先得考虑一个代码编写的问题，在大多数加密实现中，出于模块化以及效率的考量，密钥编排作为一个整体性的、前置的步骤，在明文的运算前就被完全算出来。以AES -128为例，Key 为 16字节，密钥编排后生成11个16字节的轮密钥，这是我们刚学的。很少有程序会在明文运算中，用到了Ki再去编排生成那16字节，而是像我们的Python代码那样，提前生成所有轮密钥，供后续明文运算时使用。在Android Native开发中而言，即K0-K10紧凑的在一块内存中，装在比如 uint8_t RoundKey[176]这样的数组里。我们将全体轮密钥称为轮密钥群，这么叫比较好听。
那么如果提供给我们一串字节数据，能否判断其为AES的轮密钥群？这里用上一篇某鱼直播软件使用unidbg算法分析里面出面的轮密钥群做样例，比如如下的176字节

0000: 30 29 28 27 26 25 24 23 22 21 00 00 00 00 00 00    0)('&%$#"!......
0010: 52 4A 4B 44 74 6F 6F 67 56 4E 6F 67 56 4E 6F 67    RJKDtoogVNogVNog
0020: 7F E2 CE F5 0B 8D A1 92 5D C3 CE F5 0B 8D A1 92    ........].......
0030: 26 D0 81 DE 2D 5D 20 4C 70 9E EE B9 7B 13 4F 2B    &...-] Lp...{.O+
0040: 53 54 70 FF 7E 09 50 B3 0E 97 BE 0A 75 84 F1 21    STp.~.P.....u..!
0050: 1C F5 8D 62 62 FC DD D1 6C 6B 63 DB 19 EF 92 FA    ...bb...lkc.....
0060: E3 BA A0 B6 81 46 7D 67 ED 2D 1E BC F4 C2 8C 46    .....F}g.-.....F
0070: 86 DE FA 09 07 98 87 6E EA B5 99 D2 1E 77 15 94    .......n.....w..
0080: F3 87 D8 7B F4 1F 5F 15 1E AA C6 C7 00 DD D3 53    ...{.._........S
0090: 29 E1 35 18 DD FE 6A 0D C3 54 AC CA C3 89 7F 99    ).5...j..T......
00A0: B8 33 DB 36 65 CD B1 3B A6 99 1D F1 65 10 62 68    .3.6e..;....e.bh

这个问题有什么意义？
一个比较小的作用在于，在重度混淆的样本里，我们没法自上而下的分析逻辑。那么如果发现某个参数指向这么一片内存，我们可能需要办法确认——这是不是编排后的轮密钥？

比较取巧的办法是验证图中橙色部分，验证w5是否等于w4^w1，w6是否等于w5^w2等等。
那么比较体系化的办法呢？我们假定上面字节流的最后十六个字节是轮密钥最后一轮，然后逆推出整个轮密钥群，两相对比，如果一致就可确认是否是轮密钥群。
在stark中进行验证，传入的参数中，B833DB3665CDB13BA6991DF165106268是假设的轮密钥（字节流最后十六字节），10为第几轮。

E:\Project\c_project\Stark>aes_keyschedule B833DB3665CDB13BA6991DF165106268 10
K00: 30292827262524232221000000000000
K01: 524A4B44746F6F67564E6F67564E6F67
K02: 7FE2CEF50B8DA1925DC3CEF50B8DA192
K03: 26D081DE2D5D204C709EEEB97B134F2B
K04: 535470FF7E0950B30E97BE0A7584F121
K05: 1CF58D6262FCDDD16C6B63DB19EF92FA
K06: E3BAA0B681467D67ED2D1EBCF4C28C46
K07: 86DEFA090798876EEAB599D21E771594
K08: F387D87BF41F5F151EAAC6C700DDD353
K09: 29E13518DDFE6A0DC354ACCAC3897F99
K10: B833DB3665CDB13BA6991DF165106268

比对后可确认一致。AES中还有一个特殊之处，第一轮子密钥就是主密钥，所以密钥就是30292827262524232221000000000000。又因为AES”第一轮子密钥就是主密钥“，所以有个更简单和易懂的办法——假设可疑内存块的前十六个字节是主密钥，做密钥编排，对比两者结果是否一致。
现在也有开源的工具可以更快找到密钥，这里推荐龙哥的Unidbg_FindKey