SHA1介绍

SHA实际上是一系列算法的统称，分别包括：SHA-1、SHA-224、SHA-256、SHA-384以及SHA-512。后面4中统称为SHA-2，事实上SHA-224是SHA-256的缩减版，SHA-384是SHA-512的缩减版。各中SHA算法的数据比较如下表，其中的长度单位均为位：

类别	MD5	SHA-1	SHA-224	SHA-256	SHA-384	SHA-512
消息摘要长度	128位(bit) 或 32字节	160位(bit)或40字节	224位(bit)或56字节	256位(bit)或64字节	384位(bit)或96字节	512位(bit)或128字节
消息长度	/	小于264位	小于264位	小于264位	小于2128位	小于2128位
分组长度	512bit	512bit	512bit	512bit	1024bit	1024bit
计算字长度	32bit	32bit	32bit	32bit	64bit	64bit
计算步骤数	64	80	64	64	80	80

SHA1哈希算法流程

消息填充

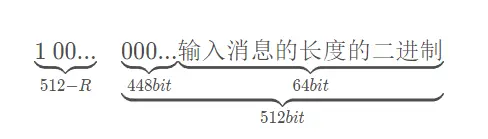
对于任意长度的明文，SHA1的明文分组过程与MD5相类似，首先需要对明文添加位数，使明文总长度为448（mod512）位。在明文后添加位的方法是第一个添加位是l，其余都是0。然后将真正明文的长度（没有添加位以前的明文长度）以64位表示，附加于前面已添加过位的明文后，此时的明文长度正好是512位的倍数。
M的长度 mod 512 = R，考虑R（R为输入消息长度按512bit进行分组后，最后一组的长度）

R < 448，在最后一组的末尾填充1个“1”及若干个“0”，使最后一组的位数达到448位；再在这448位的基础上填充64位，这64位是M的原始长度的[二进制]

R >= 448，在最后一组的末尾填充1个“1”及若干个“0”，使最后一组位数达到512；再新增一组，添加448个“0”和64位M的原始长度的二进制表示。

初始化模值

A=0x67452301

B=0xEFCDAB89

C=0x98BADCFE

D=0x10325476

E=0xC3D2E1F0

分组

第一个512位分组进来后，以32位为一组，分别存储在W0 ，……，W15 中

之后还要将这16份子明文分组扩充到80份子明文分组，我们记为W[k]（k= 0, 1,……79），扩充的方法如下。

分组扩展为80份

Wt = Mt , 当0≤t≤15

Wt=(Wt −16 ⊕ Wt −14 ⊕ Wt −8 ⊕ Wt −3)<<<1 (16≤t≤79)

“<<<” 表示循环左移符号，上述中是循环左移1位。

计算信息摘要

Kt (0≤t≤19) = 0x5A827999

Kt (20≤t≤39) = 0x6ED9EBA1

Kt (40≤t≤59) = 0x0x8F188CDC

Kt (60≤t≤79) = 0x0xCA62C1D6

4轮80步的计算中使用到的函数和固定常熟如下表所示：

计算轮次	计算的步数	计算函数	计算常数
第一轮	0≤t≤19步	ft(B,C,D)=(B&C)\|(~B&D)	_K_t=0x5A827999
第二轮	20≤t≤39步	ft(B,C,D)=B⊕C⊕D	_K_t=0x6ED9EBA1
第三轮	40≤t≤59步	ft(B,C,D)=(B&C)\|(B&D)\|(C&D)	_K_t=0x8F188CDC
第四轮	60≤t≤79步	ft(B,C,D)=B⊕C⊕D	_K_t=0xCA62C1D6

（&是与（And），|是或（Or），~是非（Not），^是异或（Xor））


&	与	两个位都为1时，结果才为1
\|	或	两个位都为0时，结果才为0
^	异或	两个位相同为0，相异为1
~	取反	0变1，1变0
<<<	循环左移	将移出的低位放到该数的高位

链接变量与初始链接变量进行求和运算

SHA1有4轮运算，每一轮包括20个步骤，一共80步，最终产生160位的信息摘要，这160位的摘要存放在5个32位的链接变量中。

在SHA1的4论运算中，虽然进行的就具体操作函数不同，但逻辑过程却是一致的。首先，定义5个变量，假设为H0、H1、H2、H3、H4，对其分别进行如下操作：

（A）、将A左移5为与函数的结果求和，再与对应的子明文分组、E以及计算常数求和后的结果赋予H0。

（B）、将A的值赋予H1。

（C）、将B左移30位，并赋予H2。

（D）、将C的值赋予H3。

（E）、将D的值赋予H4。

（F）、最后将H0、H1、H2、H3、H4的值分别赋予A、B、C、D

A = H0 = A<<<5+ft(B,C,D)+E+Wt+Kt

B = H1 = A

C = H2 = B<<<30

D = H3 = C

E = H4 = D

这一过程表示如下：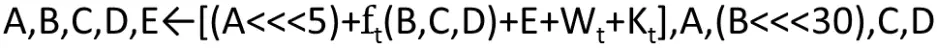

加上初始化模值

a = H0+A

b = H1+B

c = H2+C

d = H3+D

e = H4+E

result = abcde

经过4论80步计算后得到的结果，再与各链接变量的初始值求和，就得到了我们最终的信息摘要。而对于有多个明文分组的，则将前面所得到的结果作为初始值进行下一明文分组的计算，最后一组的512位分组经过80轮的操作后，最终产生的

H0、H1、H2、H3、H4要加上一开始的A、B、C、D、E，及加完后最终的abcde即为消息M的hash值。

整个sha1加密简要过程如下：

（1）将512位的明文分组划分为16个子明文分组，每个子明文分组为32位。

（2）申请5个32位的链接变量，记为A、B、C、D、E。

（3） 16份子明文分组扩展为80份。

（4） 80份子明文分组进行4轮运算。

（5）链接变量与初始链接变量进行求和运算。

（6）链接变量作为下一个明文分组的输入重复进行以上操作。

（7）最后，5个链接变量要加上一开始的模值，最终级联起来的数据就是SHA1摘要。

例子：对409732112进行sha1

409732112==>ASCII 34 30 39 37 33 32 31 31 32
转为二进制就是 4*18 = 72bit
34 ==> 0011 0100
30 ==> 0011 0000
39 ==> 0011 1001
37 ==> 0011 0111
33 ==> 0011 0011
32 ==> 0011 0010
31 ==> 0011 0001
31 ==> 0011 0001
32 ==> 0011 0010
72bit填充1000….到448bit，填充1个1和375个0

0011 0100 0011 0000 0011 1001 0011 0111 0011 0011 0011 0010 0011 0001 0011 0001 0011 0010 1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

对应16进制
34 30 39 37 33 32 31 31 32 80 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
512bit - 448bit = 64bit

留的那64比特长度，用于填充长度信息，长度单位为比特
64bit附加长度信息（就是明文对应16进制的长度）
00 …. 00 72（中间58个0, 明文72是十进制，需要转为十六进制）
明文72bit+填充（10…）376bit+长度信息（00 00 …48）64bit = 512bit
34 30 39 37 33 32 31 31 32 80 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 48
512bit / 4 = 128位16进制
128分16组 = 8位（每组8位）
W0 = 0x 34 30 39 37
W1 = 0x 33 32 31 31
W2 = 0x 32 80 00 00
W3 = 0x 00 00 00 00
…
W14 = 0x 00 00 00 00
W15 = 0x 00 00 00 48
扩展分组到80份

Wt=( Wt − 16 ⊕ Wt −14 ⊕ Wt −8 ⊕ Wt −3)<<1 (16≤_t_≤79)
这里手算前3个，最终80份程序生成
W16 = (W0⊕W2⊕W8⊕W13)<<1
W17 = (W1⊕W3⊕W9⊕W14)<<1
W18 = (W2⊕W4⊕W10⊕W15)<<1

W0 = 0011 0100 0011 0000 0011 1001 0011 0111
W1 = 0011 0011 0011 0010 0011 0001 0011 0001
W2 = 0011 0010 1000 0000 0000 0000 0000 0000
W3=0，W4=0，W8=0，W9=0，W10=0，W13=0，W14 = 0
W15= 0000 0000 0000 0000 0000 0000 0100 1000
W16 = (W0⊕W2)<<1= 0000 1101 0110 0000 0111 0010 0110 1110 = 0x 0D60726E
W17 = W1<<1= 0110 0110 0110 0100 0110 0010 0110 0010 = 0x 66646262
W18 = (W2⊕W15)<<1= 0110 0101 0000 0000 0000 0000 1001 0000 = 0x 65000090

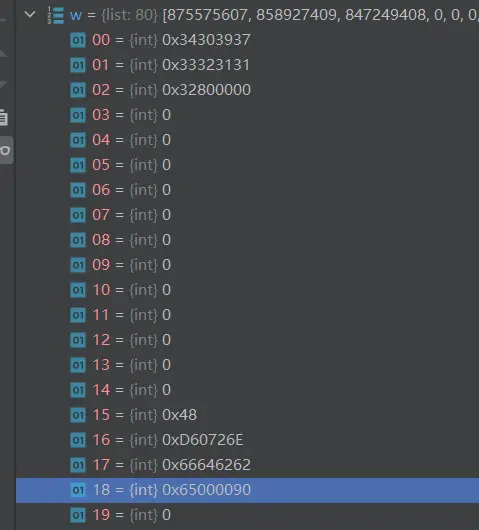
跟程序结果一致，下面直接输出结果
W0 = 0x34303937
W1 = 0x33323131
W2 = 0x32800000
W3 = 0x0
W4 = 0x0
W5 = 0x0
W6 = 0x0
W7 = 0x0
W8 = 0x0
W9 = 0x0
W10 = 0x0
W11 = 0x0
W12 = 0x0
W13 = 0x0
W14 = 0x0
W15 = 0x48
W16 = 0xd60726e
W17 = 0x66646262
W18 = 0x65000090
W19 = 0x1ac0e4dc
W20 = 0xccc8c4c4
W21 = 0xca000120
W22 = 0x3581c9b8
W23 = 0x99918919
W24 = 0x8ec0e69d
W25 = 0xa7cb57b4
W26 = 0xf9231313
W27 = 0x28000483
W28 = 0xd60726e0
W29 = 0x664624f6
W30 = 0x21c37eaa
W31 = 0x53e59ba6
W32 = 0x1cd612b
W33 = 0xf5595f41
W34 = 0x61c99c2
W35 = 0xf21b00a9
W36 = 0xb42ee9bb
W37 = 0x67966a1a
W38 = 0xd132a24c
W39 = 0xb3235961
W40 = 0x2371fd7e
W41 = 0x57415c75
W42 = 0x3437eaa1
W43 = 0x3e59bb45
W44 = 0x2957db08
W45 = 0xcc047fd6
W46 = 0x9eca0d11
W47 = 0x79908d1c
W48 = 0xd148f483
W49 = 0x9d921d19
W50 = 0xff2a2f89
W51 = 0xf5384aea
W52 = 0xa3b31bcd
W53 = 0xcf36c649
W54 = 0x33623193
W55 = 0x7c83278a
W56 = 0x12704a2a
W57 = 0x8fd19775
W58 = 0x3d927355
W59 = 0x2a2b88a6
W60 = 0x37feb543
W61 = 0x8e608fac
W62 = 0xad96814e
W63 = 0x5efe0599
W64 = 0x64e43d19
W65 = 0x95da8390
W66 = 0x7fea8510
W67 = 0xe9827238
W68 = 0x65ea391a
W69 = 0x847fd6fe
W70 = 0xca0d119e
W71 = 0x908d18f9
W72 = 0x9ef3a531
W73 = 0xf45b1bbb
W74 = 0xca16b7ff
W75 = 0xa675a007
W76 = 0x17b22d58
W77 = 0x3defd669
W78 = 0x4a141b9d
W79 = 0x98376750

80轮运算
A = 0x67452301 = 0110 0111 0100 0101 0010 0011 0000 0001
B = 0xEFCDAB89 = 1110 1111 1100 1101 1010 1011 1000 1001
C = 0x98BADCFE = 1001 1000 1011 1010 1101 1100 1111 1110
D = 0x10325476 = 0001 0000 0011 0010 0101 0100 0111 0110
E = 0xC3D2E1F0 = 1100 0011 1101 0010 1110 0001 1111 0000

计算轮次	计算的步数	计算函数	计算常数
第一轮	0≤t≤19步	ft(B,C,D)=(B&C)\|(~B&D)	_K_t=0x5A827999
第二轮	20≤t≤39步	ft(B,C,D)=B⊕C⊕D	_K_t=0x6ED9EBA1
第三轮	40≤t≤59步	ft(B,C,D)=(B&C)\|(B&D)\|(C&D)	_K_t=0x8F188CDC
第四轮	60≤t≤79步	ft(B,C,D)=B⊕C⊕D	_K_t=0xCA62C1D6

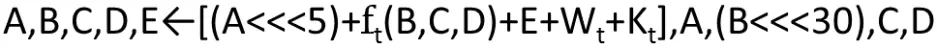
第一轮第一步
A<<<5 ==> 1110 1000 1010 0100 0110 0000 0010 1100
B&C = 1000 1000 1000 1000 1000 1000 1000 1000
B&D= 0001 0000 0011 0010 0101 0100 0111 0110
ft(B,C,D) = (B&C)|(B&D) = 1001 1000 1011 1010 1101 1100 1111 1110
H0 = 0x2D3E4D1EA（保留末8位）= 0x D3E4D1EA
H1 = 0x67452301
H2 = 0x7BF36AE2
H3 = 0x98BADCFE
H4 = 0x10325476
把H0-H4重新赋值给A,B,C,D,E
A = H0
B = H1
C = H2
D = H3
E = H4
…
第80轮
A = 0x135B4514 = 0001 0011 0101 1011 0100 0101 0001 0100
B = 0xCE03E912 = 1100 1110 0000 0011 1110 1001 0001 0010
C = 0xD50D5F9A = 1101 0101 0000 1101 0101 1111 1001 1010
D = 0xD940C253 = 1101 1001 0100 0000 1100 0010 0101 0011
E = 0x36F72811 = 0011 0110 1111 0111 0010 1000 0001 0001

A<<<5 = 0110 1011 0110 1000 1010 0010 1000 0010
ft(B,C,D)=B⊕C⊕D = 1100 0010 0100 1110 0111 0100 1101 1011
W79 = 0x98376750
K79 = 0xCA62C1D6
H0 = 0xC7486894
H1 = 0x135B4514
H2 = 1011 0011 1000 0000 1111 1010 0100 0100 = 0xB380FA44
H3 = 0xD50D5F9A
H4 = 0xD940C253

最后的H0-H4要加上一开始的模值
a = H0+A = 0x2E8D8B95
b = H1+B =0x0328F09D
c = H2+C = 0x4C3BD742
d = H3+D = 0xE53FB410
e = H4+E = 0x9D13A443
abcde = 2E8D8B950328F09D4C3BD742E53FB4109D13A443
2e8d8b950328f09d4c3bd742e53fb4109d13a443
结果一致

python实现sha1

# 0xffffffff is used to make sure numbers dont go over 32

def chunks(messageLength, chunkSize):
    chunkValues = []
    for i in range(0, len(messageLength), chunkSize):
        chunkValues.append(messageLength[i:i + chunkSize])

    return chunkValues


def leftRotate(chunk, rotateLength):
    return ((chunk << rotateLength) | (chunk >> (32 - rotateLength))) & 0xffffffff


def sha1Function(message):
    # initial hash values
    h0 = 0x67452301
    h1 = 0xEFCDAB89
    h2 = 0x98BADCFE
    h3 = 0x10325476
    h4 = 0xC3D2E1F0

    messageLength = ""

    # preprocessing
    for char in range(len(message)):
        messageLength += '{0:08b}'.format(ord(message[char]))

    temp = messageLength
    messageLength += '1'

    while (len(messageLength) % 512 != 448):
        messageLength += '0'

    messageLength += '{0:064b}'.format(len(temp))
    chunk = chunks(messageLength, 512)

    for eachChunk in chunk:
        words = chunks(eachChunk, 32)
        w = [0] * 80
        for n in range(0, 16):
            w[n] = int(words[n], 2)

        for i in range(16, 80):
            # sha1
            w[i] = leftRotate((w[i - 3] ^ w[i - 8] ^ w[i - 14] ^ w[i - 16]), 1)
            # sha0
            # w[i] = (w[i - 3] ^ w[i - 8] ^ w[i - 14] ^ w[i - 16])

            # Initialize hash value for this chunk:
        a = h0
        b = h1
        c = h2
        d = h3
        e = h4

        # main loop:
        for i in range(0, 80):
            if 0 <= i <= 19:
                f = (b & c) | ((~b) & d)
                k = 0x5A827999

            elif 20 <= i <= 39:
                f = b ^ c ^ d
                k = 0x6ED9EBA1

            elif 40 <= i <= 59:
                f = (b & c) | (b & d) | (c & d)
                k = 0x8F1BBCDC

            elif 60 <= i <= 79:
                f = b ^ c ^ d
                k = 0xCA62C1D6

            a, b, c, d, e = ((leftRotate(a, 5) + f + e + k + w[i]) & 0xffffffff, a, leftRotate(b, 30), c, d)

        h0 = h0 + a & 0xffffffff
        h1 = h1 + b & 0xffffffff
        h2 = h2 + c & 0xffffffff
        h3 = h3 + d & 0xffffffff
        h4 = h4 + e & 0xffffffff

    return '%08x%08x%08x%08x%08x' % (h0, h1, h2, h3, h4)

if __name__ == '__main__':
    plainText = "409732112"
    sha1Hash = sha1Function(plainText)
    print(sha1Hash)