对称加密算法DES的原理及分析

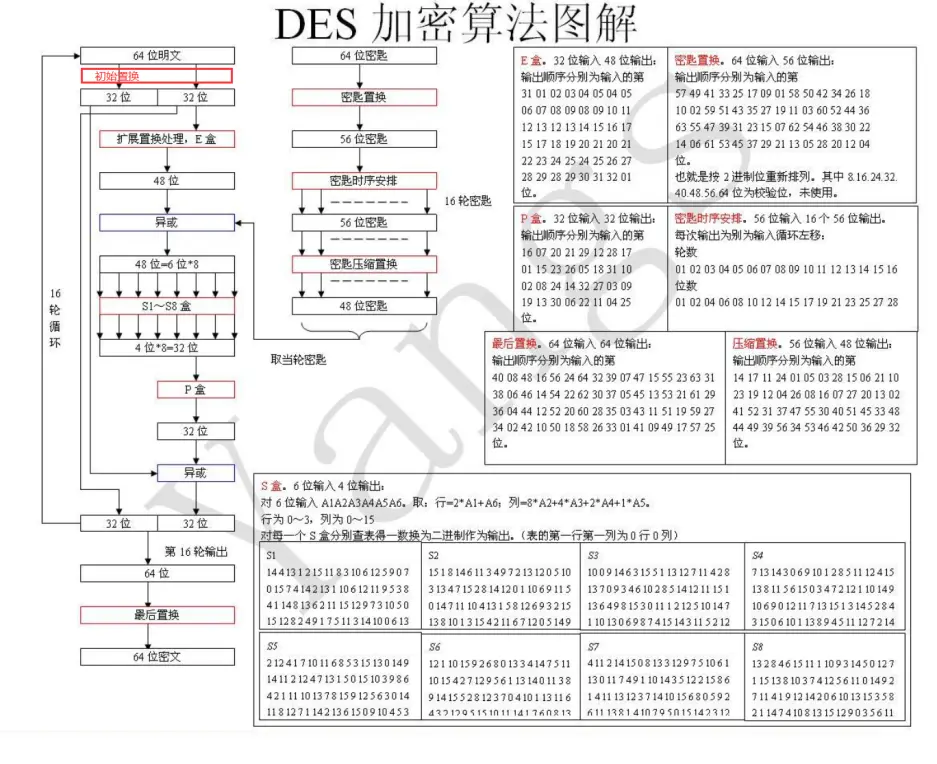
图解

手算DES

入参：
明文：64比特（16个十六进制数、8个字节）
KEY：64比特（16个十六进制数、8个字节）
出参：64比特（16个十六进制数、8个字节）

明文：0123456789ABCDEF（hex）
密钥：133457799BBCDFF1（hex）
结果：85e813540f0ab405fdf2e174492922f8
因为模式的原因，会进行填充，这里先把结果当成 85e813540f0ab405（hex）

1.对明文初始置换（重排）

PI置换表（IP表）

PI = [58, 50, 42, 34, 26, 18, 10, 2,
      60, 52, 44, 36, 28, 20, 12, 4,
      62, 54, 46, 38, 30, 22, 14, 6,
      64, 56, 48, 40, 32, 24, 16, 8,
      57, 49, 41, 33, 25, 17, 9, 1,
      59, 51, 43, 35, 27, 19, 11, 3,
      61, 53, 45, 37, 29, 21, 13, 5,
      63, 55, 47, 39, 31, 23, 15, 7]

根据置换表的索引对明文进行重新排列（例如明文第58的位置放到第一位）
明文 0123456789ABCDEF（hex）
转为二进制 00000001 00100011 01000101 01100111 10001001 10101011 11001101 11101111
重新排列后 11001100 00000000 11001100 11111111 11110000 10101010 11110000 10101010
排列顺序如图所示：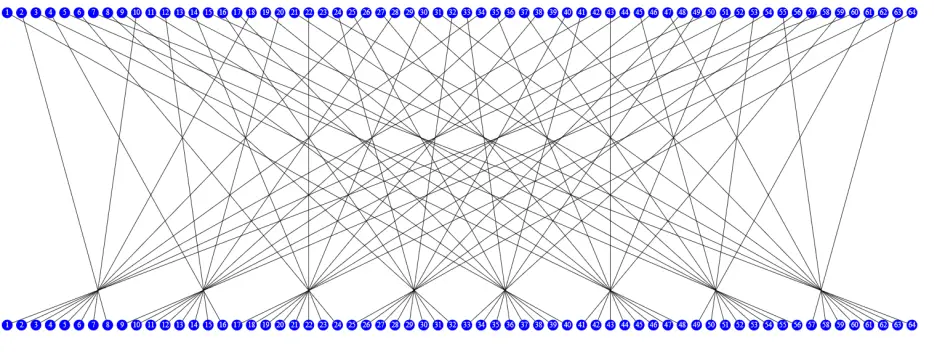

2.对密钥进行编排

PC1（CP_1）（置换选择一表）

CP_1 = [57, 49, 41, 33, 25, 17, 9,
        1, 58, 50, 42, 34, 26, 18,
        10, 2, 59, 51, 43, 35, 27,
        19, 11, 3, 60, 52, 44, 36,
        63, 55, 47, 39, 31, 23, 15,
        7, 62, 54, 46, 38, 30, 22,
        14, 6, 61, 53, 45, 37, 29,
        21, 13, 5, 28, 20, 12, 4]

密钥：133457799BBCDFF1（hex）
转为二进制：00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001
重新排列后：1111000 0110011 0010101 0101111 0101010 1011001 1001111 0001111
对DES来说，密钥64位，只有56位被使用，每8个比特的最后一位被舍弃掉
对重新编排后的拆分成左右两部分
L0：1111000 0110011 0010101 0101111
R0：0101010 1011001 1001111 0001111

3.对编排后的密钥进行16轮循环左移生成16个子密钥

对L0和R0进行16轮循环左移，每轮根据上一轮左移n位+本次左移的位数（或者是本次左移索引+前面左移索引位数），左移后加在一起LnRn，然后根据PC2（CP_2）表重新编排为K，只有48位，生成16个子密钥（注：索引是从1开始）。

生成的16个子密钥subkeys会对应明文处理16轮每轮的key

1	SHIFT = [1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1]

CP_2 = [14, 17, 11, 24, 1, 5, 3, 28,
        15, 6, 21, 10, 23, 19, 12, 4,
        26, 8, 16, 7, 27, 20, 13, 2,
        41, 52, 31, 37, 47, 55, 30, 40,
        51, 45, 33, 48, 44, 49, 39, 56,
        34, 53, 46, 42, 50, 36, 29, 32]

L1：1110000 1100110 0101010 1011111
R1：1010101 0110011 0011110 0011110
L1R1：1110000 1100110 0101010 1011111 1010101 0110011 0011110 0011110
编排后K1：00011011 00000010 11101111 11111100 01110000 01110010

第二次左移2位（对L0和R0左移2位，或者对L1和R1左移1位）
L2：1100001 1001100 1010101 0111111
R2：0101010 1100110 0111100 0111101
L2R2：1100001 1001100 1010101 0111111 0101010 1100110 0111100 0111101
编排后K2：01111001 10101110 11011001 11011011 11001001 11100101

第三次左移4位（对L0和R0左移4位，或者对L2和R2左移2位）
L3：0000110 0110010 1010101 1111111
R3：0101011 0011001 1110001 1110101
L3R3：0000110 0110010 1010101 1111111 0101011 0011001 1110001 1110101
编排后K3：010101 011111 110010 001010 010000 101100 111110 011001
…

K1 = 000110 110000 001011 101111 111111 000111 000001 110010
K2 = 011110 011010 111011 011001 110110 111100 100111 100101
K3 = 010101 011111 110010 001010 010000 101100 111110 011001
K4 = 011100 101010 110111 010110 110110 110011 010100 011101
K5 = 011111 001110 110000 000111 111010 110101 001110 101000
K6 = 011000 111010 010100 111110 010100 000111 101100 101111
K7 = 111011 001000 010010 110111 111101 100001 100010 111100
K8 = 111101 111000 101000 111010 110000 010011 101111 111011
K9 = 111000 001101 101111 101011 111011 011110 011110 000001
K10 = 101100 011111 001101 000111 101110 100100 011001 001111
K11 = 001000 010101 111111 010011 110111 101101 001110 000110
K12 = 011101 010111 000111 110101 100101 000110 011111 101001
K13 = 100101 111100 010111 010001 111110 101011 101001 000001
K14 = 010111 110100 001110 110111 111100 101110 011100 111010
K15 = 101111 111001 000110 001101 001111 010011 111100 001010
K16 = 110010 110011 110110 001011 000011 100001 011111 110101

4.对明文进行16轮运算加密

明文重新编排后的 11001100 00000000 11001100 11111111 11110000 10101010 11110000 10101010
拆分成左右两部分
L0：11001100 00000000 11001100 11111111
R0：11110000 10101010 11110000 10101010
每一轮运算只对R进行改变
加密：
Li+1=Ri
Ri+1=Li⊕F(Ri,Ki)

解密：
Ri=Li+1
Li=Ri+1⊕F(Li+1,Ki)

f函数： 1. f函数首先将输入经过E表扩展置换，将32位的输入扩展为48位。
2. 将48位结果与第i轮第密钥ki进行XOR(异或)操作
3. 将异或操作第结果送入S盒进行压缩，压缩成32位
4. 将32位的结果送入P盒置换

Expand表

E = [32, 1, 2, 3, 4, 5,
     4, 5, 6, 7, 8, 9,
     8, 9, 10, 11, 12, 13,
     12, 13, 14, 15, 16, 17,
     16, 17, 18, 19, 20, 21,
     20, 21, 22, 23, 24, 25,
     24, 25, 26, 27, 28, 29,
     28, 29, 30, 31, 32, 1]

S盒（S_BOX，8组）

S_BOX = [    
[[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
 [0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
 [4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
 [15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],
],

[[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
 [3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
 [0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
 [13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],
],

[[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
 [13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
 [13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
 [1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],
],

[[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
 [13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
 [10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
 [3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],
],  

[[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
 [14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
 [4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
 [11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],
], 

[[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
 [10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
 [9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
 [4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],
], 

[[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
 [13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
 [1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
 [6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],
],
   
[[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
 [1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
 [7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
 [2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11],
]
]

P盒

P = [16, 7, 20, 21, 29, 12, 28, 17,
     1, 15, 23, 26, 5, 18, 31, 10,
     2, 8, 24, 14, 32, 27, 3, 9,
     19, 13, 30, 6, 22, 11, 4, 25]

第一轮为例：
R1= L0⊕f(R0，K1)
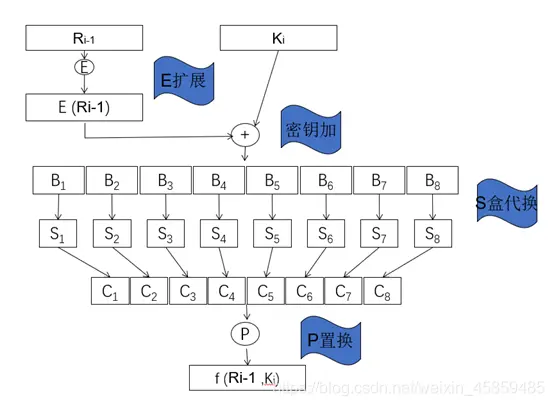
F函数 P(S(E(Ri)⊕Ki))：
R0：11110000 10101010 11110000 10101010
经过E表编排：01111010 00010101 01010101 01111010 00010101 01010101
与K1异或后：011000 010001 011110 111010 100001 100110 010100 100111

把异或后的拆分8组，进行8轮S盒运算

B1 = 011000
B2 = 010001
B3 = 011110
B4 = 111010
B5 = 100001
B6 = 100110
B7 = 010100
B8 = 100111

将每一组前后1个比特拼接为row转十进制，中间4个比特为column转十进制，然后去S盒映射第i个row行column列

B1 0 1100 0
row：00 ==> 0 （十进制）
column：1100 ==> 12 （十进制）
(0, 12) ==> S[0][0][12]==>5
B1 = 5 ==> 0101 （二进制）

B2 0 1000 1
row：01 ==> 1 （十进制）
column：1000 ==> 8 （十进制）
(1, 8) ==> S[1][1][8]==>12
B1 =12==> 1100（二进制）

B3 0 1111 0
row：00 ==> 0 （十进制）
column：1111==> 15 （十进制）
(0, 15) ==> S[2][0][15]==>8
B1 =8==> 1000（二进制）
…
68=48bit 经过8轮 48=32bit
把B1-B8拼接起来：
01011100 10000010 10110101 10010111

经过P盒置换后：00100011 01001010 10101001 10111011
F函数结束，结果异或L0
R1：11101111 01001010 01100101 01000100
L1：R0
…
16轮后
R16：00001010 01001100 11011001 10010101
L16：01000011 01000010 00110010 00110100
R16L16拼接（R在前），再经过末置换表（PI_1）（64位）：
R16L16：00001010 01001100 11011001 10010101 01000011 01000010 00110010 00110100
置换后：10000101 11101000 00010011 01010100 00001111 00001010 10110100 00000101
转为hex就是结果了：85e813540f0ab405

PI_1表

PI_1 = [40, 8, 48, 16, 56, 24, 64, 32,
        39, 7, 47, 15, 55, 23, 63, 31,
        38, 6, 46, 14, 54, 22, 62, 30,
        37, 5, 45, 13, 53, 21, 61, 29,
        36, 4, 44, 12, 52, 20, 60, 28,
        35, 3, 43, 11, 51, 19, 59, 27,
        34, 2, 42, 10, 50, 18, 58, 26,
        33, 1, 41, 9, 49, 17, 57, 25]

分组密码的填充

Passing只用于CBC和ECB模式，默认采用PKCS#7进行填充

DES 64比特明文，64比特密钥，结果64比特输出
那为什么明文刚好是64比特，如果输入是56比特？20比特？或者什么都不输入呢？
明文会切割成每64比特为一组进行des加密，最后一组小于或等于64都会进行填充
如果传入的是utf，需先转hex

小于64比特：

123456789（hex）==> 1234567809（hex）

还差6位hex（3个字节），填充030303：1234567809030303

123456789abcd（hex）==>123456789abc0d（hex）
还差2位hex（1个字节），填充01：123456789abc0d01

等于64比特，需要填充一整个分组0808080808080808：
0123456789abcdef（hex）==> 0123456789abcdef0808080808080808

最少填充一字节，最多填充一整个分组，不能不填充。

分组密码的工作模式

ECB

相同的分组输入，计算后的结果是完全一致的，每个分组单独处理，叫ECB工作模式
这种模式有很多好处，我们可以直接for 循环，将很长的输入分成对应个数的分组，每个分组得到结果后拼接在一起就行，而且这也意味着可以并行计算。
如果ECB模式是可行的、安全的，那么我们一定选择它，因为最简单和高效。那也就不会出现别的工作模式了，可惜的是它并不安全。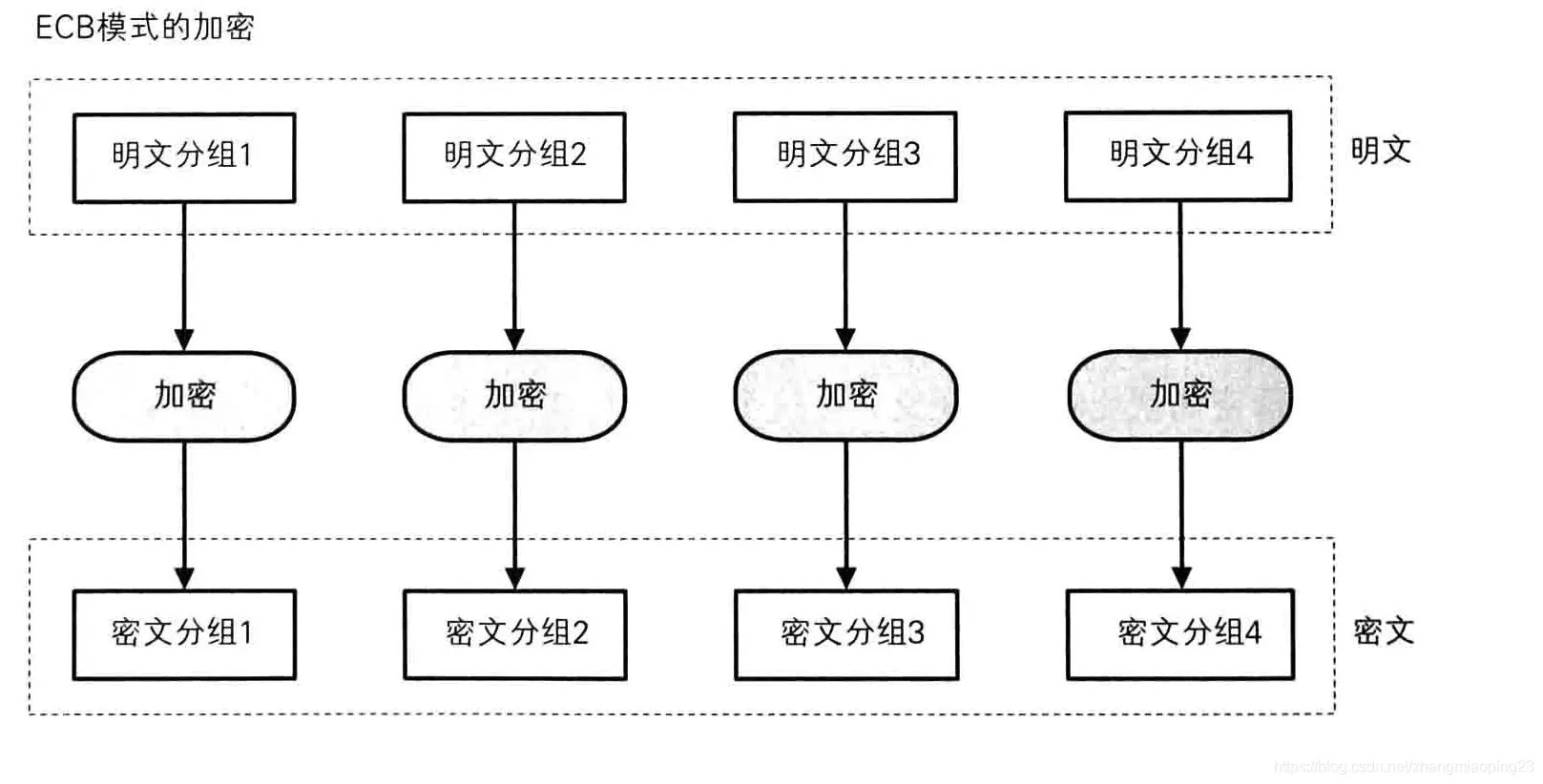

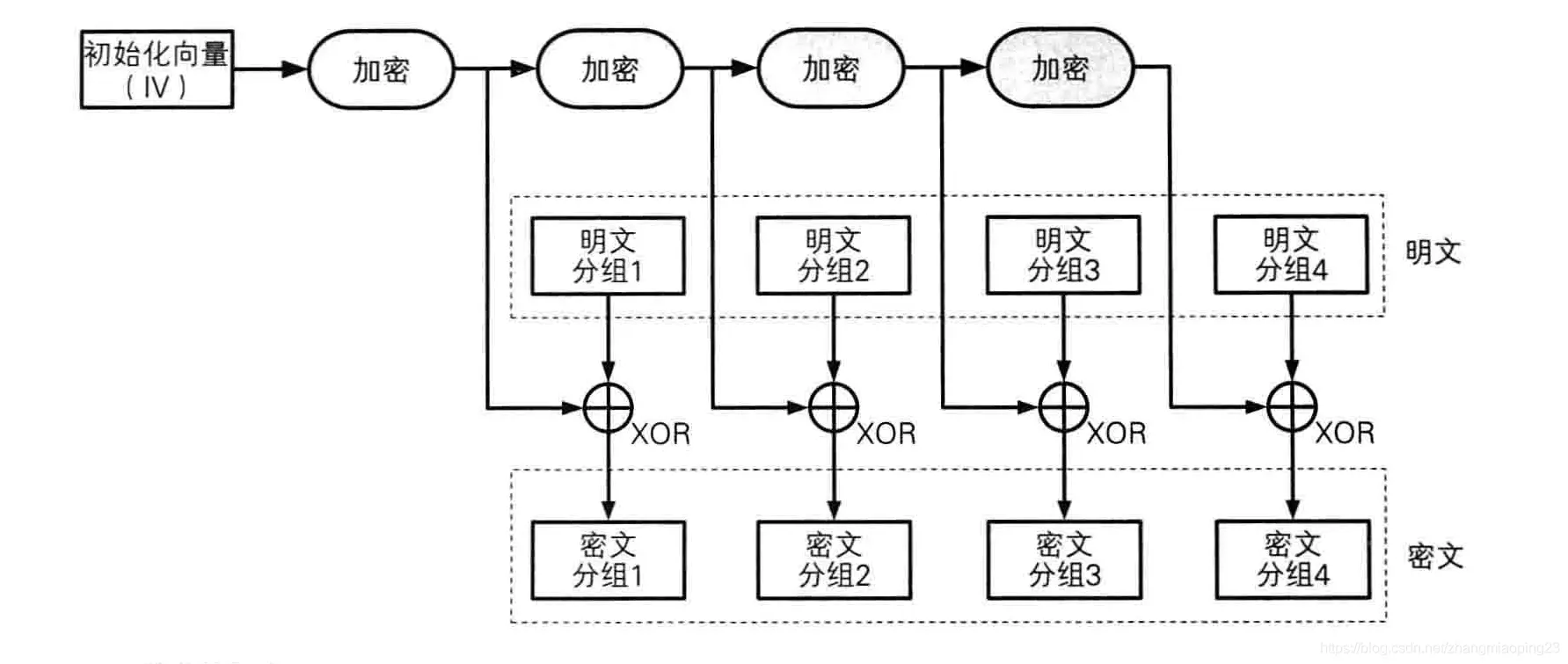
CBC

最常用的模式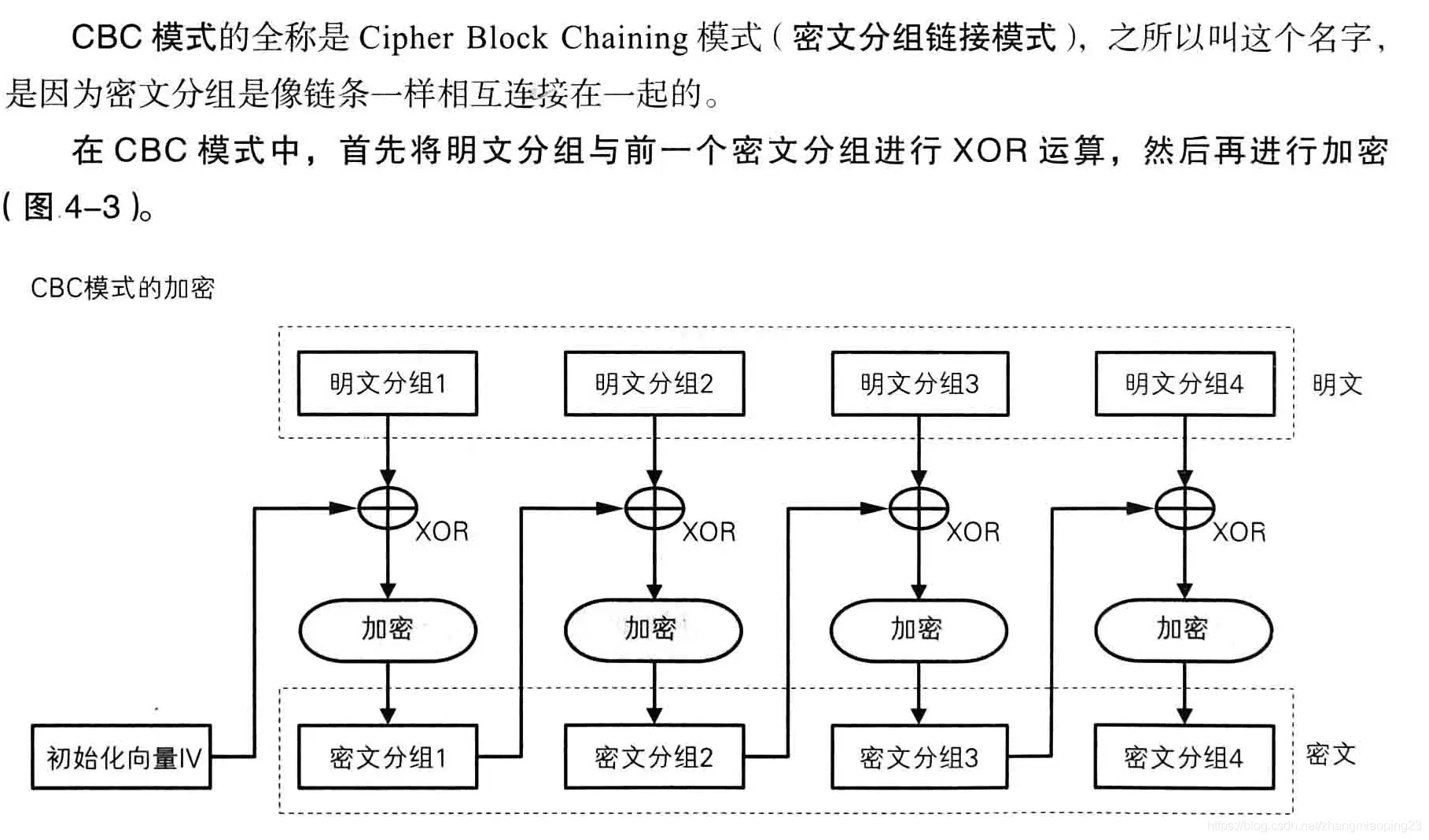

其实想法也很朴素，每个明文分组在加密前多一个步骤，和上一个分组的密文块进行异或运算。因为第一个明文块没有所谓的“上一个分组的密文块“，所以需要人给一个64比特，或者说8字节的输入，我们叫它初始化向量，IV。
在cyberchef中验证一下

明文：123456789ABCDEF0（hex）

密钥：133457799BBCDFF1（hex）

使用CBC模式

IV：0123456789ABCDEF

计算结果：0ecb68bac16aece07cbadcfa7a974bcc（hex）

按照我们上面的说法

0ecb68bac16aece0的明文应该就是123456789ABCDEF0和0123456789ABCDEF异或的结果

得到结果1317131f1317131f

使用cyberchef计算123456789ABCDEF0 ^ 0123456789ABCDEF 得到结果1317131f1317131f，单独计算其DES加密结果，注意这儿要用ECB模式: 0ecb68bac16aece0 fdf2e174492922f8，因为1317131f1317131f是一个分组的长度，所以要填充0808080808080808， fdf2e174492922f8是08的结果，所以不用管。可以发现，第一块加密结果0ecb68bac16aece0正是我们所预期的。

接下来看一下第二块，第二块即0808080808080808，按照CBC的规则计算 0ecb68bac16aece0 ^ 0808080808080808 = 06c360b2c962e4e8，单独计算ECB下的06c360b2c962e4e8 结果为7cbadcfa7a974bcc fdf2e174492922f8，第二块结果7cbadcfa7a974bcc也完全正确。

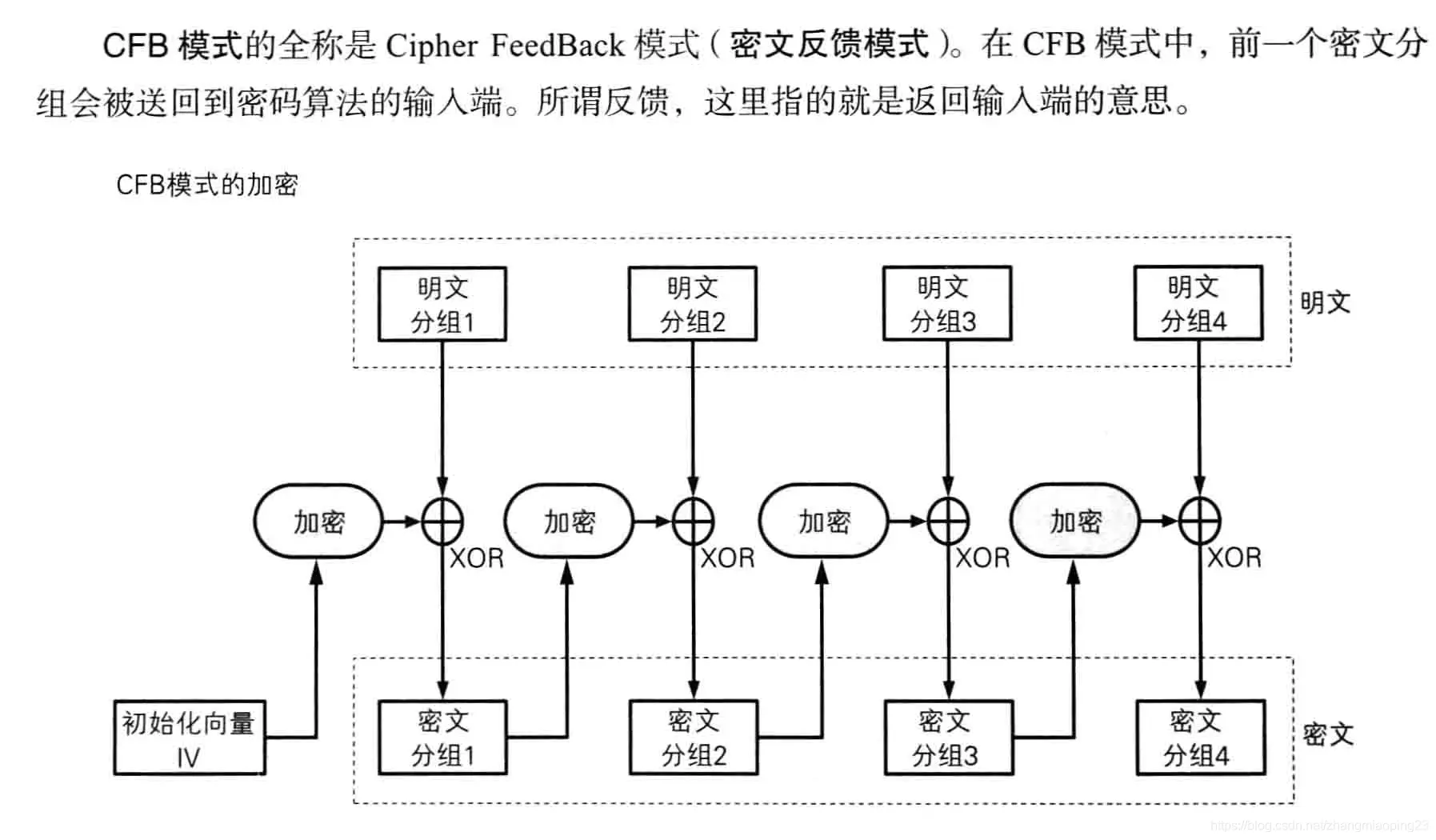
CFB

明文：123456789ABCDEF0

密钥：133457799BBCDFF1

IV：0123456789ABCDEF

模式：CFB

结果: 97dc452c95b66af5

IV即0123456789ABCDEF的des加密结果85e813540f0ab405

85e813540f0ab405 与 123456789ABCDEF0 的异或结果是97dc452c95b66af5

OFB

明文：123456789ABCDEF0

密钥：133457799BBCDFF1

IV：0123456789ABCDEF

模式：OFB

结果: 97dc452c95b66af5

即一个分组的OFB与CFB是一样一样的

两个分组的计算：

明文：123456789ABCDEF0 123456789ABCDEF0

密钥：133457799BBCDFF1

IV：0123456789ABCDEF

模式：OFB

结果：97dc452c95b66af5 759a2c51fb637db5

直接观察第二个分组759a2c51fb637db5是如何计算出来呢?
它是明文和加密两次的IV的异或结果
明文：123456789ABCDEF0 加密第一次：85e813540f0ab405 加密第二次 67ae7a2961dfa345f，最后异或 67ae7a2961dfa345f ^ 123456789ABCDEF0 = 759a2c51fb637db5

图解