对称加密算法AES的原理及分析
zsk Lv4
  2022-12-27 23:14:10 2022-12-27 23:14   2022-12-27 23:14:10    4.3k 字  19 分钟  

image

AES算法简述

分组加密有几种方式分别是：

ECB：是一种基础的加密方式，密文被分割成分组长度相等的块（不足补齐），然后单独一个个加密，一个个输出组成密文。将整个明文分成若干段相同的小段，然后对每一小段进行加密
00112233445566778899aabbccddee 还差2位hex（1个字节），填充01：00112233445566778899aabbccddee01
00112233445566778899aabbccddeeff 等于128比特，需要填充一整个分组：00112233445566778899aabbccddeeff(hex)==> 00112233445566778899aabbccddeeff10101010101010101010101010101010
最少填充一字节，最多填充一整个分组，不能不填充。

CBC：是一种循环模式，前一个分组的密文和当前分组的明文异或操作后再加密，这样做的目的是增强破解难度。先将明文切分成若干小段，然后每一小段与初始块或者上一段的密文段进行异或运算后，再与密钥进行加密

CFB/OFB实际上是一种反馈模式，目的也是增强破解的难度。密码算法的输出（指密码key而不是密文）会反馈到密码算法的输入中，OFB模式并不是通过密码算法对明文直接加密，而是通过将明文分组和密码算法的输出进行XOR来产生密文分组。

ECB和CBC的加密结果是不一样的，两者的模式不同，而且CBC会在第一个密码块运算时加入一个初始化向量。


AES-128接收16字节的明文输入，16字节的密钥，输出16字节的密文结果。

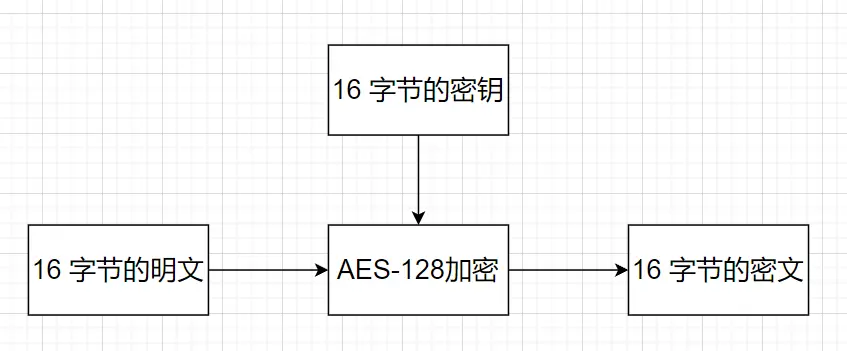
image

入参：
明文：128比特（32个十六进制数、16个字节）
KEY：128比特（32十六进制数、16个字节）
出参：128比特（32个十六进制数、16个字节）

明文：7a68656e677368616f6b756e79796473（hex）
密钥：0123456789abcdef0123456789abcdef（hex）

下方是整体流程图：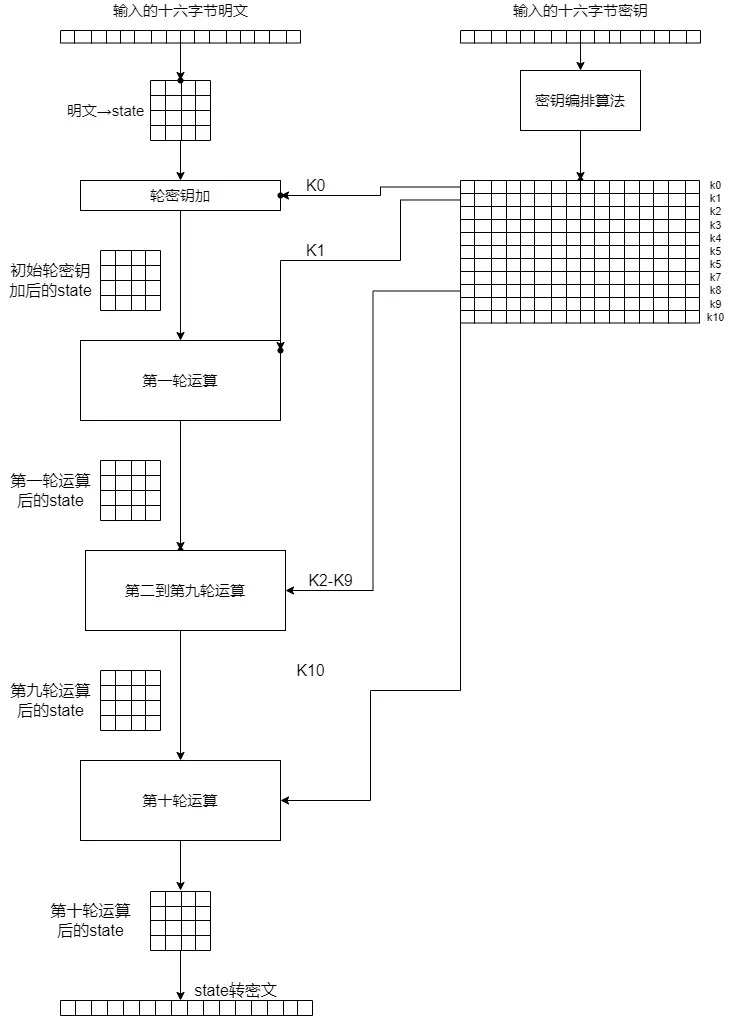

image

首先看整体的流程图，我们发现，AES的整体图景可以分成左右两块，即明文的处理和密钥的编排。明文的处理主体是一个初始化轮密钥加和十轮运算，在初始化轮密钥加十轮运算中都需要使用密钥编排的结果。密钥编排将16个字节经过运算推演出11组轮密钥，每一组16个字节，称之为K0,K1,K2…K10

密钥编排

下面我们看一下密钥扩展是如何算出来的，这是我们的密钥Key 0123456789abcdef0123456789abcdef。为了区分密钥和密钥编排后的轮密钥，我们将此时的密钥叫主密钥。

在AES-128中，密钥扩展后得16*11共176字节，使用时逐十六个字节划分成K0,K1,…K10使用，但是在生成时，它是逐四个字节生成的，即44*4。我们不妨用数组来描述它，即一个包含了44个元素的数组,叫W。

这四十四个元素的生成规则有三种，如下图所示：

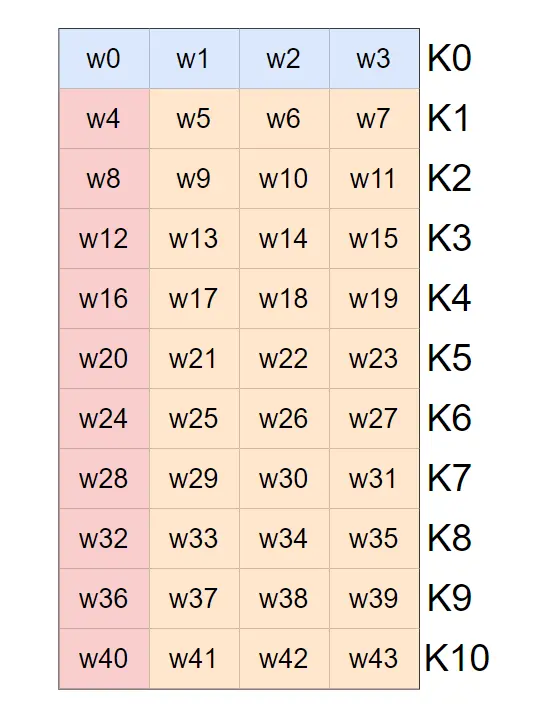
image

不同颜色代表了不同规则。最上方的W0,W1,W2,W3 就是主密钥本身切成四段。
Key = 0123456789abcdef0123456789abcdef
W0 = 01234567
W1 = 89abcdef
W2 = 01234567
W3 = 89abcdef

左侧的红色部分，W4,W8,W12,….W40的生成复杂一点。
Wn=g(Wn−1) xor Wn−4
xor 是异或运算，比如 W4=g(W3) xor W0。g(当前元素前面那个元素) 异或 当前元素头顶上那个元素。

那么关键点就是这个 g 函数了， g 函数一共三个步骤——循环左移、S盒替换、字节异或。 我们以W4运算中所需的W3为例。
W3=89abcdef

g函数——循环左移、S盒替换、字节异或

循环左移

首先是循环左移，规则固定—— 将最左边的一个字节挪到右边即可

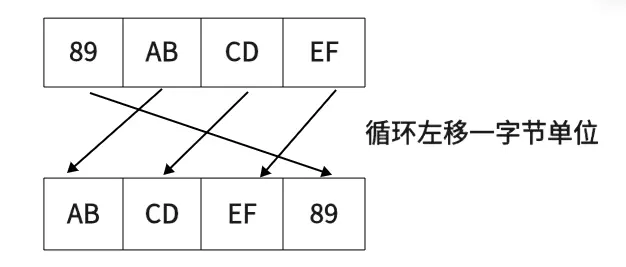
image


循环左移后为 abcdef89

S盒替换

第二步是S盒替换，S盒替换听着很高级，但操作上很简单——将数值本身作为索引取出S数组中对用的值。S盒是固定的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
SBox = [
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16
]

num = 0xab
result = SBox[num]
print(hex(result))
# 0x62

S盒的背后有十分复杂的知识，但好在我们并不需要去了解。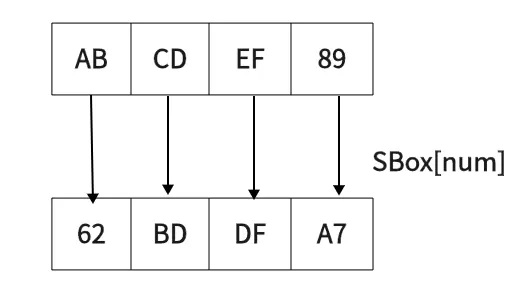

image


AB CD EF 89 经过S盒替换后为 62 BD DF A7

最高字节和一个固定常量异或

最后一个步骤更简单，将上一步结果中的最高字节和一个固定常量异或。W4的生成是第一个，用如下rcon表的第一个元素0x1。W40即第十次，用最后一个元素0x36.

1
2
rcon = [0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36]
#        W4    W8    W12   W16   W20   W24   W28   W32   W36   W40

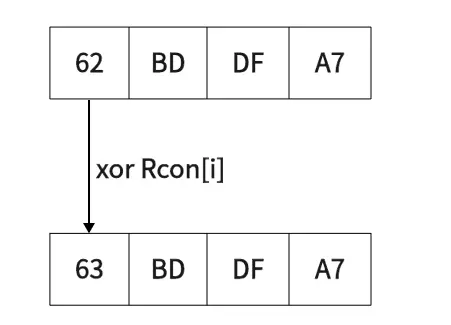
image


62 BD DF A7 最高位62与rcon第一个元素，即0x01异或后为：63 BD DF A7
W4 = g(W3) xor W0
= g(0x89abcdef) xor 0x01234567
= 0x63BDDFA7 xor 0x01234567
= 0x629e9ac0
最后一步可以直接用python算: 

1
print(hex(0x63BDDFA7 ^ 0x01234567))

上图中蓝色和红色的部分都讲完了，那么橙色部分呢？相当的简单，和红色部分类似，去掉g函数即可
Wn=Wn−1 xor Wn−4
打个比方，W5 = W4 ^ W1 = 0x629e9ac0 ^ 0x89abcdef = 0xeb35572f

如下是完整的密钥编排部分的Python代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
Sbox = (
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)

Rcon = (0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36)


def text2matrix(text):
    matrix = []
    for i in range(16):
        byte = (text >> (8 * (15 - i))) & 0xFF
        if i % 4 == 0:
            matrix.append([byte])
        else:
            matrix[i // 4].append(byte)
    return matrix


def shiftRound(array, num):
    '''

    :param array: 需要循环左移的数组
    :param num: 循环左移的位数
    :return: 使用Python切片，返回循环左移num个单位的array
    '''
    return array[num:] + array[:num]


def g(array, index):
    '''
    g 函数
    :param array: 待处理的四字节数组
    :index:从1-10，每次使用Rcon中不同的数
    '''
    # 首先循环左移1位
    array = shiftRound(array, 1)
    # 字节替换
    array = [Sbox[i] for i in array]
    # 首字节和rcon中对应元素异或
    array = [(Rcon[index] ^ array[0])] + array[1:]
    return array


def xorTwoArray(array1, array2):
    '''
    返回两个数组逐元素异或的新数组
    :param array1: 一个array
    :param array2: 另一个array
    :return:
    '''
    assert len(array1) == len(array2)
    return [array1[i] ^ array2[i] for i in range(len(array1))]


def showRoundKeys(kList):
    for i in range(len(kList)):
        print("K%02d:" %i +"".join("%02x" % k for k in kList[i]))


def keyExpand(key):
    master_key = text2matrix(key)
    round_keys = [[0] * 4 for i in range(44)]
    # 规则一(图中红色部分)
    for i in range(4):
        round_keys[i] = master_key[i]
    for i in range(4, 4 * 11):
        # 规则二(图中红色部分)
        if i % 4 == 0:
            round_keys[i] = xorTwoArray(g(round_keys[i - 1], i // 4), round_keys[i - 4])
        # 规则三(图中橙色部分)
        else:
            round_keys[i] = xorTwoArray(round_keys[i - 1], round_keys[i - 4])
    # 将轮密钥从44*4转成11*16,方便后面在明文的运算里使用
    kList = [[] for i in range(11)]
    for i in range(len(round_keys)):
        kList[i//4] += round_keys[i]

    showRoundKeys(kList)
    return kList


input_bytes = 0x00112233445566778899aabbccddeeff
key = 0x2b7e151628aed2a6abf7158809cf4f3c
kList = keyExpand(key)

运行结果如下

1
2
3
4
5
6
7
8
9
10
11
K00:0123456789abcdef0123456789abcdef
K01:629e9ac0eb35572fea16124863bddfa7
K02:1a00c63bf13591141b23835c789e5cfb
K03:154ac987e47f5893ff5cdbcf87c28734
K04:385dd190dc228903237e52cca4bcd5f8
K05:4d5e90d9917c19dab2024b1616be9eee
K06:c355b89e5229a144e02bea52f69574bc
K07:a9c7dddcfbee7c981bc596caed50e276
K08:7a5fe58981b199119a740fdb7724edad
K09:570a707cd6bbe96d4ccfe6b63beb0b1b
K10:8821df9e5e9a36f31255d04529bedb5e

我们对AES密钥编排部分的学习就基本完成了。

明文运算

现在开始学习明文的运算，即图中左边的部分。首先，我们要调整明文的格式，在AES中，数据以state的形式计算、中间存储和传输，中文名即状态。
从明文转到state形式很简单，以我们的明文7a68656e677368616f6b756e79796473为例。从上到下，从左到右。千万不要颠倒顺序，第一行不是“7a 68 65 6e”。除此之外，state中的数，我们一般用十六进制表示，且不加0x前缀，这样看着比较舒服。除非特意强调是十进制，否则下文均为十六进制。

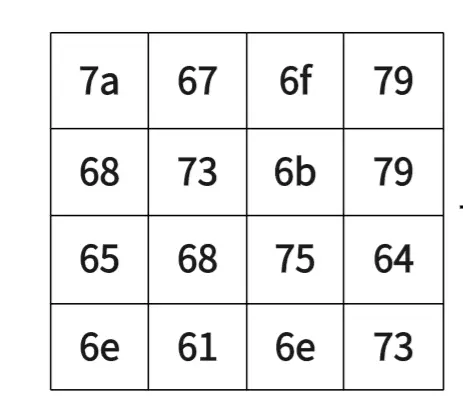
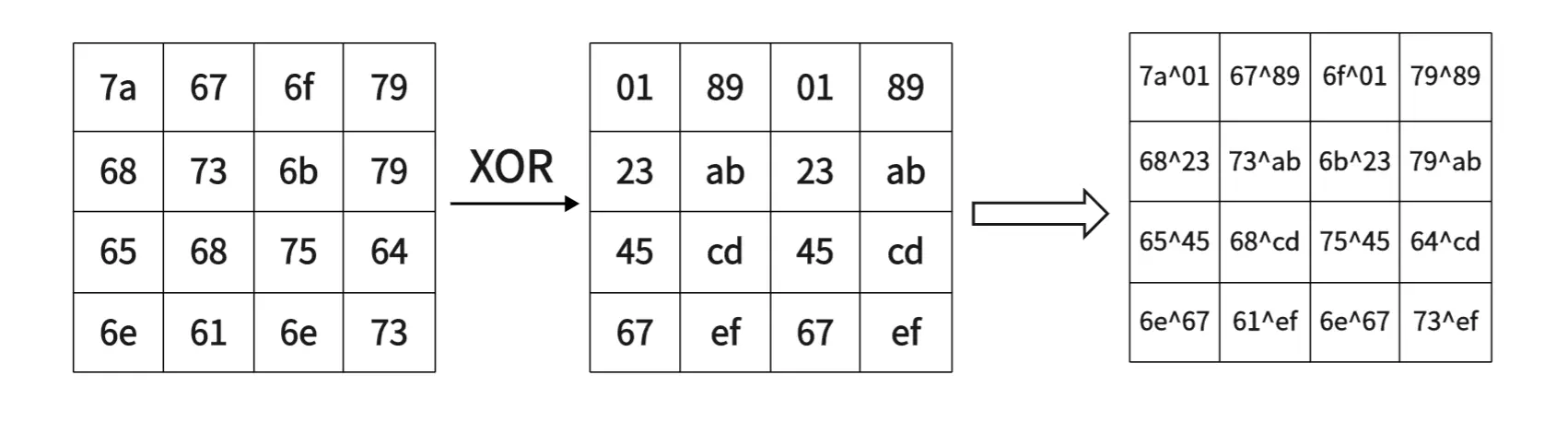
image


接下来是轮密钥加步骤，因为是第一次轮密钥加步骤，所以也叫初始轮密钥加。轮密钥加步骤听着很怪，但实质很简单。只需要将对应的轮密钥和 一样从上到下，从左到右排列。两个矩阵逐字节异或，这就是轮密钥加步骤。为什么要叫轮密钥加而不是轮密钥异或？我们卖个关子，后面再说。
初始的轮密钥加使用 K0 ，0123456789abcdef0123456789abcdef。

image


接下来就是十轮主运算，看如下的伪代码，我们可以清楚看到一轮运算中有什么，以及第十轮和前九轮有什么区别。

image


初始的明文转和最后的转明文自不必说，然后是初始轮密钥，使用 K0 。
前九轮运算中，包含四个步骤： 字节替换，循环左移，列混淆，轮密钥加。
第十轮中，包含三个步骤：字节替换，循环左移，轮密钥加。相比前九轮缺一个列混淆，其余相同。
十轮运算中的轮密钥加，和初始轮密钥加相比，除了使用的轮密钥不同外，并无不同，分别为K1…..K10。
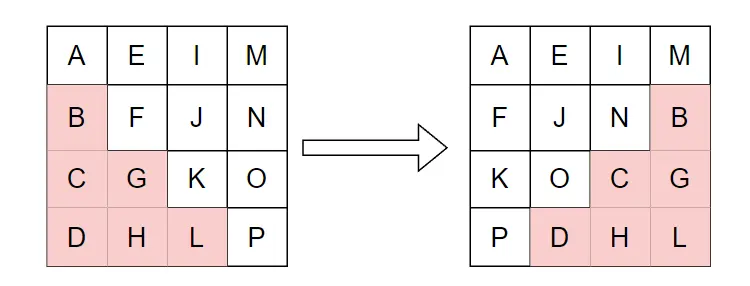
而 字节替换步骤，和密钥编排中的S盒替换完全一致。
即循环左移，和密钥编排中的循环左移类似，但有差异。密钥编排中， g 函数中也需循环左移，但其中待处理的数据仅有一行，而明文编排中 是四行。
其循环左移规则如下：第一行不循环左移，第二行循环左移1字节，第三行循环左移2字节，第四行循环左移3字节。

image


相对复杂的是列混淆步骤，列混淆步骤涉及两块知识，1是矩阵乘法，2是伽罗瓦域的加法和乘法。前者还好，后者属于抽象代数的内容，比较复杂。
先看第一块——矩阵乘法。首先演示简单的矩阵相乘，

左边准备相乘的两个矩阵，我们称它俩为矩阵A和矩阵B，如何求结果矩阵中的abcd ？规则如下：第m行第n列的值等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
a是第一行第一列，那么就是A的第一行和B的第一列元素乘积之和

同理可得



即


所谓乘积之和，指乘法和加法。
再来看AES列混淆中的矩阵乘法，我们的 ，左边乘如下所示固定矩阵



看起来有些复杂，小例子中是2*2的矩阵要算4个值，这里是4*4的矩阵要算16个值。我们这里只管第一列，其他列的计算类似。


列混淆中的的加法和乘法并不是小例子或日常中的那样，其中的加法指 异或运算 。2A + 3B + C + D 即 2A ^ 3B ^ C ^ D，这也是 叫轮密钥加而不是轮密钥异或的原因——加法就是异或。那么其中的乘法呢？乘法复杂一些，想真正理解的可以网上冲浪搜索伽罗瓦域内乘法。我们这里仅考虑如下三种情况，因为AES-128加密中，列混淆的乘法中，仅涉及这三个数。 结合Python代码可以更清晰，函数名中 mul 是multiply（乘）的缩写。

x * 1，结果为x本身

1
2
def mul_by_01(num):
    return num

x * 2，首先切换到二进制形式，最高位为0时，比特串左移1比特，最右边补0即可。如果最高位为1，比特串左移1比特，最右边补0，最后再异或上 0x1B

1
2
3
4
5
6
7
def mul_by_02(num):
    if num < 0x80:
        res = (num << 1)
else:
    res = (num << 1) ^ 0x1b

    return res % 0x100

x * 3 = (x * 02) + x，注意”加“是异或哦。

1
2
def mul_by_03(num):
    return (mul_by_02(num) ^ num)

列混淆，就这么讲完了。下面看完整的AES代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
Sbox = (
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)

Rcon = (0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36)


def text2matrix(text):
    matrix = []
    for i in range(16):
        byte = (text >> (8 * (15 - i))) & 0xFF
        if i % 4 == 0:
            matrix.append([byte])
        else:
            matrix[i // 4].append(byte)
    return matrix


def shiftRound(array, num):
    '''

    :param array: 需要循环左移的数组
    :param num: 循环左移的位数
    :return: 使用Python切片，返回循环左移num个单位的array
    '''
    return array[num:] + array[:num]


def g(array, index):
    '''
    g 函数
    :param array: 待处理的四字节数组
    :index:从1-10，每次使用Rcon中不同的数
    '''
    # 首先循环左移1位
    array = shiftRound(array, 1)
    # 字节替换
    array = [Sbox[i] for i in array]
    # 首字节和rcon中对应元素异或
    array = [(Rcon[index] ^ array[0])] + array[1:]
    return array


def xorTwoArray(array1, array2):
    '''
    返回两个数组逐元素异或的新数组
    :param array1: 一个array
    :param array2: 另一个array
    :return:
    '''
    assert len(array1) == len(array2)
    return [array1[i] ^ array2[i] for i in range(len(array1))]


def showRoundKeys(round_keys):
    # 将轮密钥从44*4转成11*16
    kList = [[] for i in range(11)]
    for i in range(len(round_keys)):
        kList[i // 4] += round_keys[i]
    for i in range(len(kList)):
        print("K%02d:" % i + "".join("%02x" % k for k in kList[i]))


def keyExpand(key):
    master_key = text2matrix(key)
    round_keys = [[0] * 4 for i in range(44)]
    # 规则一(图中红色部分)
    for i in range(4):
        round_keys[i] = master_key[i]
    for i in range(4, 4 * 11):
        # 规则二(图中红色部分)
        if i % 4 == 0:
            round_keys[i] = xorTwoArray(g(round_keys[i - 1], i // 4), round_keys[i - 4])
        # 规则三(图中橙色部分)
        else:
            round_keys[i] = xorTwoArray(round_keys[i - 1], round_keys[i - 4])
    showRoundKeys(round_keys)
    return round_keys


def AddRoundKeys(state, roundKey):
    result = [[] for i in range(4)]
    for i in range(4):
        result[i] = xorTwoArray(state[i], roundKey[i])

    return result


def SubBytes(state):
    result = [[] for i in range(4)]
    for i in range(4):
        result[i] = [Sbox[i] for i in state[i]]
    return result


def ShiftRows(s):
    s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]
    return s


def mul_by_02(num):
    if num < 0x80:
        res = (num << 1)
    else:
        res = (num << 1) ^ 0x1b
    return res % 0x100


def mul_by_03(num):
    return mul_by_02(num) ^ num


def MixColumns(state):
    for i in range(4):
        s0 = mul_by_02(state[i][0]) ^ mul_by_03(state[i][1]) ^ state[i][2] ^ state[i][3]
        s1 = state[i][0] ^ mul_by_02(state[i][1]) ^ mul_by_03(state[i][2]) ^ state[i][3]
        s2 = state[i][0] ^ state[i][1] ^ mul_by_02(state[i][2]) ^ mul_by_03(state[i][3])
        s3 = mul_by_03(state[i][0]) ^ state[i][1] ^ state[i][2] ^ mul_by_02(state[i][3])
        state[i][0] = s0
        state[i][1] = s1
        state[i][2] = s2
        state[i][3] = s3

    return state


def state2Text(state):
    text = sum(state, [])
    return "".join("%02x" % k for k in text)


def encrypt(input_bytes, kList):
    '''

    :param input_bytes: 输入的明文
    :param kList: K0-K10
    :return:
    '''
    plainState = text2matrix(input_bytes)
    # 初始轮密钥加
    state = AddRoundKeys(plainState, kList[0:4])
    for i in range(1, 10):
        state = SubBytes(state)
        state = ShiftRows(state)
        state = MixColumns(state)
        state = AddRoundKeys(state, kList[4 * i:4 * (i + 1)])

    state = SubBytes(state)
    state = ShiftRows(state)
    state = AddRoundKeys(state, kList[40:44])
    return state


input_bytes = 0x7a68656e677368616f6b756e79796473
key = 0x0123456789abcdef0123456789abcdef
kList = keyExpand(key)
cipherState = encrypt(input_bytes, kList)
cipher = state2Text(cipherState)
print(cipher)



对称加密算法AES的原理及分析
posts/57259/
作者
zsk
发布于
2022-12-27 23:14
许可
 评论
  1. 1. AES算法简述
  2. 2. 密钥编排
    1. 2.1. g函数——循环左移、S盒替换、字节异或
      1. 2.1.1. 循环左移
      2. 2.1.2. S盒替换
      3. 2.1.3. 最高字节和一个固定常量异或
  3. 3. 明文运算